pomocy! Julka: W narożniku prostokątnego trawnika o wymiarach 3m x 7m wbito kołek, do którego przywiązano na sznurku żarłoczną kozę. Wykaż, że długość x sznurka pozwalająca kozie na zjedzenie trawy dokładnie z połowy trawnika spełnia nierówność 2√3 < x < 3√2.

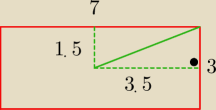
the foxi: ile wynosi długość zielonej linii (sznurka, którym ograniczona jest koza)?

Julka: ale dlaczego wysnaczyles taki zielony prostkat? to przeciez nie jest polowa trawnika.

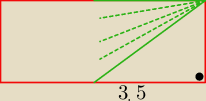
the foxi: jeśli połowę trawnika rozpatrzymy jako każdy możliwy punkt, który przechodzi przez symetralną dłuższego boku, otrzymamy długości sznurka należące do przedziału [3.5;√22.25] część liczb z danego przedziału spełnia tę nierówność, a część nie, więc uważam, że chodzi o środek trawnika gdy uznamy, że połową trawnika jest każdy punkt leżący na symetralnej krótszego boku, również otrzymamy długości wykraczające poza przedział (2√3;3√2)

the foxi: już wiem, co jest źle w moim rozumowaniu. początkowo rozumiałem polecenie jako "na środku trawnika jest odrobina trawy. wykaż, że..."

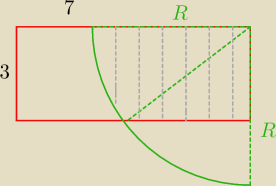
ite: Julka, oblicz pole wyjedzone przez kozę na sznurku o długości 2√3 oraz na sznurku dług.3√2.

	21
Sprawdź, czy jedna wielkość będzie większa a druga mniejsza niż		m2.
	2

ite: @foxi wg mnie "połowa trawnika", to połowa powierzchni trawnika, ale zaczynam mieć wątpliwości

the foxi: 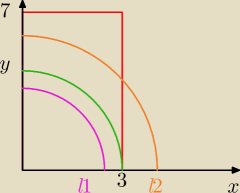ite, może jednak o to chodziło ale nie ukrywam, dość skomplikowane rachunki l>0

	πl2		π*32
ile trawy zje koza, gdy sznur będzie miał długość 3? P=		=		≈7.069
	4		4

mniej niż połowa, tak więc sznurek musi być dłuższy zatem czas wytoczyć cięższe działo, czyli całkę równanie okręgu o środku w punkcie S(0;0): x²+y²=l² ⇒ y=±√l²−x²

	l2		x		x√l2−x2
∫√l2−x2dx=		*arcsin(		)+		+C
	2		l		2

"pole" trawy zjedzonej przez kozę to ∫√l²−x²dx w granicach od 0 do 3

	l2		x		x√l2−x2
(granice: 0 do 3) ∫√l2−x2dx=[		*arcsin(		)+		+C]30=
	2		l		2

l2

3

3√l2−9

l2

0

0*√l2−0

=

*arcsin(

)+

+C−

*arcsin(

)+

−C=

2

l

2

2

l

2

l2

3

3√l2−9

l2

3

3√l2−9

=

*arcsin(

)+

−0+0=

*arcsin(

)+

2

l

2

2

l

2

l2		3		3√l2−9
	*arcsin(		)+		=10.5 (połowa pola prostokąta)
2		l		2

	3
l2*arcsin(		)+3√l2−9=21
	l

po wpisaniu do wolframa otrzymałem l≈3.9256

the foxi: oczywiście l należy do danego przedziału, co było do wykazania, aczkolwiek pewnie był prostszy sposób a ja, jak zwykle, poleciałem na około

ite: może wystarczy suma: pole wycinka koła i pole trójkąta

Mila: Trzeba zapytać Julki jaki poziom edukacji. Wg mnie zrobić, jak sugeruje ite o 17:09, jeżeli to LO.

PW: Oczywiście, przecież nie kazali nam liczyć dokładnej długości sznurka, lecz sprawdzić poprawność oszacowania.