nierówności wielomianowe lox: Rozwiąż nierówności. a) x⁴ − x³ − 7x² + x + 6 ≥ 0 b) x⁴ − x³ + 2x − 1 < 0 c) x⁴ − 5x³ + 10x² − 8x > 0 d) x⁴ − x³ + 2x − 1 < 0 Proszę bo kompletnie tego nie rozumiem. Mamy wypisywać jakieś krotności, dzielić przez dwumiany, potem zaznaczać na osi jakoś dziwnie sinusoidalnie, nigdy nie wiem kiedy od dołu a kiedy od góry.. i pisać wynik....

Bleee: Co do końcówki Twoich problemow: https://matematykaszkolna.pl/strona/142.html

Jolanta: sprawdzam dzielniki liczby 6 ,dla którego z nich wynik =0 W(1)=1−1−7+1+6=0 czyli wielomian dzieli sie przez x−1 x³ −7x−6 x⁴−x³−7x²+x+6 : (x−1) −x⁴+x³ −7x²+x 7x²−7x −6x+6 6x−6 x³−7x−6=0 dla x=−2 x²−2x−3 x³−7x−6 : (x+2) −x³−2x² −2x²−7x 2x²+4x −3x−6 3x+6 x²−2x−3=0 Δ=b²−4ac=4+12=16

	−b−√Δ		2−4
x1=		=		=−1
	2a		2

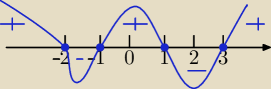
x₂=3 miejsca zerowe wielomianu 1, −2 , −1 ,3 zaznaczasz je na osi i rysujesz od prawej strony z góry ponieważ przy najwyższej potedze jest plus x⁴ pierwiastki nie powtarzają sie więc przechodzisz na drugą stronę osi .patrzysz gdzie wykres jest na i nad osią

Mila: Schemat Hornera: x⁴ − x³ − 7x² + x + 6 ≥ 0 W(1)=1−1−7+1+6=0 schemat Hornera: x=1 1 −1 −7 1 6 1 0 −7 −6 0 x⁴−x³−7x+x+6=(x−1)*(x³−7x−6) P(x)=x³−7x−6 P(1)=1−7−6≠0 P(−1)=−1+7−6=0 ⇔P(x) dzieli się przez x+1 1 0 −7 −6 x=−1 1 −1 −6 0 P(x)=x²−x−6 x²−x−6=0 Δ=25 x=−2 lub x=3 x∊{−2,−1,1,3} współczynnik przy x⁴ a=1>0 zaczynamy rysować falę od góry Odp: x∊(−∞,−2>∪<−1,1>∪<3,∞)