Prosta nierówność trygonometryczna Aga: Proste nierówności trygonometryczne Czy mógłby mi ktoś dobrze rozpisać taki przykład? sin(pi/6−x)>= −√3\2 w przedziale <−pi,2pi>

PW: Matematycy nie znają pojęcia "rozpisać". W dziedzinie muzyki jestem ignorantem, ale słyszałem, że można utwór rozpisać na poszczególne grupy instrumentów (partytura?). Ten dyrygent to ma ręce pełne roboty, żeby wszystko zgrać w czasie. ta−da−da−dam (trąby) ta−da−da−dam (trąby i kotły jednocześnie) ta−da−da−dam−da−dam (smyczkowe)

Mizia: Dziękuję za twoją nieocenioną pomoc i zaangażowanie w pomoc drugiej osobie.

PW: Mizia, ty jeteś Aga obrażona, czy wypowiadasz sią w imienu uciśnionych? Sama "rozpisz".

Mizia: Nie jestem obrażona. Prosiłam o pomoc, a ty potraktowałeś mnie ironicznie, łapiąc za słówka.

Janek191:

Leszek: Mozna takie nierownosci rozwiazywac : Niech y = π/6 − x wowczas : sin y ≥ −√3/2 I na podstawie zasadniczego wykresu dla funkcji f(y) = sin y obliczamy przedzialy dla y , i nastepnie wracamy do zmiennej x , powodzenia !

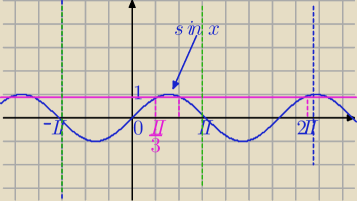
Mila: zał. x∊<−π,2π>

	−√3
sin(pi/6−x)≥		⇔
	2

	π		−√3
−sin(x−		)≥		/*(−1)
	6		2

	π		√3
sin(x−		)≤
	6		2

Najpierw rozwiązujemy w przedziale <−π,π>

	π		π		2π		π		π
−π+2kπ≤(x−		)≤		+2kπ lub		+2kπ≤(x−		)≤π+2kπ /+
	6		3		3		6		6

	5π		π		5π		7π
−		+2kπ≤x≤		+2kπ lub		+2kπ≤x≤		+2kπ
	6		2		6		6

Teraz postawiamy kolejno za k liczby całkowite i sprawdzamy, czy czy mieścimy się w podanym przedziale k=0

	5π		π		5π		7π
(1) −		≤x≤		lub (2)		≤x≤		zgadza się
	6		2		6		6

k=1

	7π
(3)		≤x≤2π ( tylko dotąd można wg zał.) lub to już nie pasuje , przekroczone 2π
	6

Teraz k=−1

	17π		3π
−		≤x≤−		nic nie pasuje przekroczona dziedzina
	6		2

	−7π		5π		5π
lub		≤x≤−		stąd mamy: (4) −π≤x≤−
	6		6		6

"Łączymy" przedziały ( najlepiej zaznacz na osi, jeśli będą kłopoty, to narysuję) (1) i (4) oraz (2) i (3)

	π		5π
−π≤x≤		lub		≤x≤2π
	2		6

======================