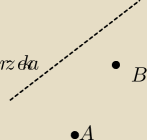
harcerze JSNZ: Harcerz musi zanieść wodę z rzeki do punktu B a wyrusza z punktu A. Jak wyznaczyć najkrótszą drogę?

a7: może to będzie pomocne: https://pl.wikipedia.org/wiki/Problem_najkr%C3%B3tszej_%C5%9Bcie%C5%BCki

!: kierunek x wzdłuż rzeki, kierunek y prostopadle do niego o zwrocie do harcerza A = (0,a) B = (d,b) punkt pobrania wody z rzeki P = (x,0) odległość AP = sqrt(x²+a²) odległość BP = sqrt((x−d)²+b²) suma odległości, którą minimalizujemy: S = AP+BP = √(x²+a²)+√((x−d)²+b²) trzeba znaleźć minimum S(x) można policzyć pochodną i przyrównać do zera to będzie punkt stacjonarny, jak druga pochodna się nie zeruje w tym punkcie to jest to ekstremum, jak jest dodatnia to jest to minimum (ale na zdrowy rozsądek maksimum to nie będzie, bo można te drogi robić dowolnie długie) Problem znalezienia tego punktu sprowadzi się do znalezienia miejsc zerowych wielomianu.

PW: Ludzie, to jest zadanie dla zdolnego ucznia klasy piątej. Odległość między dowolnym punktem P na brzegu rzeki a punktem B jest taka sama jak między P a B' − symetrycznym względem rzeki obrazem B. Narysować inny rysunek: A, rzeka, B' i będzie widać od razu, gdzie jest punkt P wyznaczający najkrótszą drogę. Oczywiście zakładamy w tym zadaniu, że szerokość rzeki nie ma znaczenia, co sugeruje szkic.

Adamm: Jedno z klasycznych zadań w geometrii. Prostota rozwiązania jest wręcz "magiczna"