problem z modułem
Tob: Witam mam problem z rozwiązaniem takowej nierówności
|x
3+5x
2|<−x
czy jakaś dobra duszyczka wytłumaczyłaby mi jak się za to zabrać?
Z góry dziękuje za pomoc

9 paź 20:45
Tadeusz:
x<0 ... (dlaczego?)
a dalej:
|x
2|*|x+5|<−x
x*{x+5|>−1
dalej... przedziały

9 paź 21:00
a7: ja mam tu taki początek
| | ⎧ | x3+5x2 gdy x3+5x2≥0 | |
| |x3+5x2| = | ⎩ | −x3+5x2 gdy x3+5x2<0 |
|
1 x
2(x+5)≥0 więc x∊<5,
∞)
2 x
2(x+5)<0 stąd x∊(−
∞, −5)
robimy pierwszy przypadek x∊<5,
∞)
x
3+5x
2+x <0
x(x
2+5x+1)<0
x=0 lub x=(−5−
√21)/2 lub x=(−5+
√21)/2
sprawdzamy na osi i wychodzi
x∊∅,
2. rozpatrujemy drugi przypadek
−x
3−5x
2+x<0
−x(x
2+5x−1)<0
x=0 lub x=(−5−
√21)/2 lub x=(−5+
√21)/2
sprawdzamy na osi
i wychodzi , że x∊
ale nie robiłam wieki takich zadań i nie jestem pewna czy dobrze naprowadzam
9 paź 21:12
Mila:
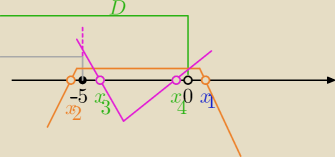
D:
x<0
|x
3+5x
2|+x<0
|x|*|x
2+5x|+x<0 (|x|=−x dla x<0)
−x*|x
2+5x|+x<0 /:x
−|x2+5x|+1>0
a)
|x
2+5x|=x
2+5x dla (x≤−5 lub x>0) i x<0⇔
wtedy dla x≤−5 mamy nierówność:
−x
2−5x+1>0
Δ=29
| | 5−√29 | | 5+√29 | |
x1= |
| >0 lub x2= |
| |
| | −2 | | −2 | |
lub
b)x>−5 i x<0
|x
2+5x|=−x
2−5x
wtedy mamy nierówność:
x
2+5x+1>0
Δ=21
| | −5−√21 | | −5+√21 | |
x3= |
| <0 lub x4= |
| <0 |
| | 2 | | 2 | |
| | −5−√21 | | (−5+√21 | |
x∊(−5, |
| )∪( |
| ,0) |
| | 2 | | 2 | |
odp:
| | −5−√29 | | −5−√21 | | (−5+√21 | |
x∊( |
| , |
| )∪( |
| ,0) |
| | 2 | | 2 | | 2 | |
==============================
9 paź 22:44


 D:
x<0
|x3+5x2|+x<0
|x|*|x2+5x|+x<0 (|x|=−x dla x<0)
−x*|x2+5x|+x<0 /:x
−|x2+5x|+1>0
a)
|x2+5x|=x2+5x dla (x≤−5 lub x>0) i x<0⇔
wtedy dla x≤−5 mamy nierówność:
−x2−5x+1>0
Δ=29
D:
x<0
|x3+5x2|+x<0
|x|*|x2+5x|+x<0 (|x|=−x dla x<0)
−x*|x2+5x|+x<0 /:x
−|x2+5x|+1>0
a)
|x2+5x|=x2+5x dla (x≤−5 lub x>0) i x<0⇔
wtedy dla x≤−5 mamy nierówność:
−x2−5x+1>0
Δ=29