Zadania z logiki. Zozol: Proszę o rozwiązanie wraz z wyjaśnieniami Będę wdzięczny za jakąkolwiek pomoc Zad.1 Udowodnić prawo Pierce'a [(p⇒q)⇒p]⇒p Zad. 2 Zdefiniować a) alternatywę za pomocą koniunkcji i negacji, b) koniunkcję za pomocą implikacji i negacji. Zad.3 Znaleźć możliwie najkrótszą formułę równoważną danej (p⋀q) ⋁ ¬(¬p⇒ ¬q) Zad. 4 Uzasadnić, że podzielność liczby całkowitej przez 2 jest warunkiem koniecznym podzielności przez 6. Czy jest to warunek wystarczający? Zad. 5 Czy dla liczby naturalnej p nie mniejszej niż pięć to, że jest liczbą pierwszą jest warunkiem wystarczającym, aby 240 dzieliło p⁵−p? Czy jest to warunek konieczny? Zad.6 Ocenić wartość logiczną zdań: a) ∀x∊ℛ ∃y∊ℛ x≠y ∧ x² = y² b) ∃x∊ℚ x²=3 c) ∀ε∊ℛ ∃n0∊ℕ ∀n∊ℕ (n≥n0 ⇒ 1/n≤ε) Zad.7 Napisać zaprzeczenia następujących zdań, a następnie ocenić wartość logiczną zdań oraz ich zaprzeczeń a) ∃x∊ℛ ∀y∊ℛ x²−y²≤0 b) ∀x∊ℛ ∃y∊ℛ ∀n∊ℕ* xy<−1/n c) ∃x∊ℛ ∀y∊ℛ ∀n∊ℕ* Zad. 8 Uzasadnić prawa de Morgana oraz prawa łączności i rozdzielności dla działań na zbiorach. Zad. 9 Napisać zaprzeczenia następujących zdań, a następnie ocenić wartość logiczną zdań oraz ich zaprzeczeń a) ∀x∊ℛ (x<0 ⇒ x²≥0) b) ∃x∊ℕ (9|x ∨ x|9) c) ∀x∊ℛ ∃y∊ℛ x²−y²<0 Zad. 10 Czy funkcja x→(x²−2x+3) jest iniekcją, suriekcją, bijekcją? (sam wzór tego nie przesądza). Prosiłbym też o wytłumaczenie o jaki wzór tu chodzi i czego nie przesądza.

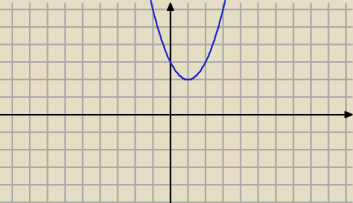Janek191: z.10 Zależy od dziedziny., np. w ( − ∞, 1) lub w ( 1, +∞) funkcja jest bijekcją.

Zozol: A mógłbyś wytłumaczyć dokładniej od czego zależy, czy to będzie suriekcja, bijekcja, czy iniekcja?

iteRacj@: wpisuj każde zadanie osobno, będzie łatwiej Zad.6 Ocenić wartość logiczną zdań: a) ∀x∊ℛ ∃y∊ℛ x≠y ∧ x² = y² prawda b) ∃x∊ℚ x²=3 fałsz c) ∀ε∊ℛ ∃n₀∊ℕ ∀n∊ℕ (n≥n₀ ⇒ 1/n≤ε) fałsz

Zozol: ok, dzięki za radę. Mam pytanko do podpunktu c)− o co chodzi z tym epsilonem i n0?