trójkąt równoramienny , dlaczego kąty przy podstawie równe a7: Dzień dobry wszystkim Mam pytanie.Jak się prawidłowo uzasadnia, że 2 kąty w trójkącie równoramiennym są równe?

a7: rysuję trójkąt równoramienny i prowadzę jego wysokość, kąt między ramionami to γ, a przy podstawie to α oraz β, i teraz zauważamy, że kąty "u góry to 90 stopni minus gamma pół, następnie stweirdzamy, że alfa i beta są im odpowiednio równe więc uzasadniliśmy czy tak?

mat: z wierzchoła, gdzie wychodzą oba ramiona opuść wysokość. Dzieli ona wyjściowy trójkąt na dwa. Jakie są te trójkąty?

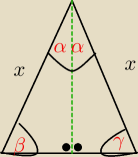
the foxi: z cechy przystawania trójkątów kąt−bok−kąt stwierdzamy, że oba mniejsze trójkąty są przystające − mają wspólne kąty 90^o, α oraz bok długości x wniosek? β=γ

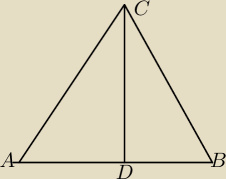
Krzysiek60 : narysuj wysokosc CD i uzasadnij ze te trojkaty sa przystajace ADC jest przystajacy do BDC

Blee: albo z tw. cosinusów

Blee: the foxi −−− a niby skąd 'wiesz' że wysokość dzieli kąt przy wierzchołku na dwa równe kąty? Przystawanie mamy z BBK (wysokość, przeciwprostokątna, kąt prosty).

the foxi: masz rację, tego jeszcze możemy nie wiedzieć

PW: mat i the foxi, Krzysiek60 − wasze dowody wychodzą z przekonania, że wysokość w trójkącie równoramiennym dzieli podstawę lub kąt przy wierzchołku na przystające (odcinki lub kąty). A skąd to wiadomo? Czy to nie jest przypadkiem tak samo nieoczywiste jak postawione pytanie o kąty przy podstawie? Takie fakty powinno się dowodzić nie za pomocą cech przystawania, lecz elementarnie. Dwa kąty są przystające, jeżeli istnieje izometria przekształcająca je na siebie nawzajem. Tutaj tą izometrią jest symetria osiowa − trzeba w ten sposób główkować. To jest tylko moje skromne zdanie, pewnie zaraz na mnie naskoczą.

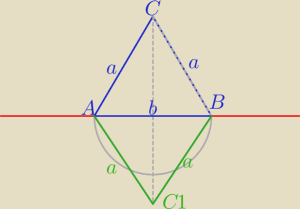
Mila: ΔABC₁ symetryczny do ΔABC względem prostej AB czworokąt ACBC₁ jest rombem, zatem: kąty przeciwległe równe przekątne są dwusiecznymi kątów wewnętrznych ∡CAB≡∡CBA

PW: Moje wyrazy uznania

Mila:

a7: tutaj chodziłoby bez odwoływania się do symetrii, gdyż symetrii na tym etapie jeszcze nie było, ale bardzo dziękuję wszystkim, zreserczowałam, że można to zrobić tak: wyznaczamy punkt D w połowie odcinka AB (podstawy) i prowadzimy odcinek CD i mamy przystawanie trójkątów BOK, BOK BOK (gdyz CD jest wspólnym bokiem, AD i DB są równe, i AC i BC sa rowne, gdyż to trójkąt równoramienny), stąd też kąty będa równe i to jest chyba ten prawidłowy sposób uzasadniania,którego szukałam (lub jeden z prawidłowych) bardzo dziękuję za wszystkie wskazówki i sposoby

a7: @Mila wczytałam się w ten dowód i już rozumiem, dziękuję serdecznie

PW: a7, nie taka jest kolejność wprowadzania pojęć i dowodzenia. Definicja jest taka jak pisałem 8 października o 22:43 − dwie figury nazywa się przystającymi, jeżeli istnieje przekształcenie izometryczne (takie, które nie zmienia odległości), w którym obrazem jednej z figur jest druga (i odwrotnie). Jednym z takich przekształceń izometrycznych jest symetria osiowa (istniejąca na zasadzie pewnika). Złożenie symetrii osiowych też jest izometrią, co łatwo wykazać. Cechy przystawania trójkątów są rzeczą wtórną − pokazujemy prawdziwość tych cech za pomocą pewnych symetrii osiowych. O symetrii osiowej mówi się bodajże w piątej klasie. Nie jest możliwe wprowadzanie cech przystawania bez symetrii osiowej, więc nie opowiadaj, że "symetrii na tym etapie jeszcze nie było". Dowód przytoczony przez Ciebie o 00:16 jest niby poprawny, dopóki ktoś nie spyta: − A skąd wiesz, że trójkąty o odpowiednio równych bokach mają odpowiednie kąty równe? Ponieważ odpowiedź na to pytanie jest tak samo trudna jak na pytanie postawione w zadaniu (nie wiesz dopóki nie zastosujesz własności symetrii), takie rozumowanie jest pseudodowodem − powoiłujesz się na twierdzenie nieoczywiste, o tym samym stopniu trudności co dowodzone.

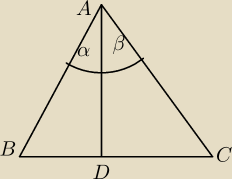
Krzysiek60 : twierdzenie : W trojkacie rownoramiennyn dwusieczna kata przy wierzcholku dzieli podsatwe na polowy Zalozenie : W trojkacie rownoramiennym ABC ∡α= ∡β (czyli AD jest dwusieczna Teza : BD= DC (czyli podsatwa zostala podzielona na polowy Dowod ; Rozpatrzmy dwa trojkaty ADB i ADC Stweirdzamy ze w tych trojkatach AB=AC jako ramiona trojkata rownoramiennego bok Ad jest wspolny ∡α=∡β z zalozenia na podsatwie cechy przystawania trojkatow (BKB) stweirdzamy ze ΔADB≡ΔADC Z rownosci tych trojkatow wynika rownosc odpowiednich elementow wiec BD= DC Dla wykazania slusznosci tego twierdzenia udowodnilismy ze trojkty ADBi ADC sa przystajace Ale z rownosci tych trojkatow wynika rowniez ze ∡B= ∡C .Odkrywamy dalsza wlasnosc trojkata rownoramiennego Wniosek. W trojkacie rownoramiennym katy przy podstawie sa rowne .

Krzysiek60 : Wniosek nr 2 . W trojkacie rownoramiennym dwusieczna kata przy wierzcholku jest prostopadla do podsatwy .

a7: dziękuję @PW nie wiedziałam, że symetria jest juz w 5 klasie, natomiast myślałam o tym co mówiłeś (że ktoś może spytać skąd wiadomo, że trójkąt o bokach równych ma kąty równe) i znalazłam dowód na to, że BOK BOK BOK to cecha przystawania trójkątów http://www.wiw.pl/matematyka/geometria/geometria_02_01.asp jednak wychodzi na to, że dowód Mili jest chyba najbardziej prawidłowy w tym sensie, że jest najbliżej pojęć pierwotnych i najmniej "na około" Dzięki wszystkim raz jeszcze PS. @Krzysiek60, chodziło mi o wykazanie ze kąty przy podstawie są równe a nie wykrycie tego przy okazji, ale jeśli to jest też dowód to super Dziękuję również