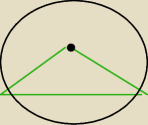
 Uwzględnij dane przedstawione na rysunku i oblicz długość cięciwy AB.
Troche mi rysunek nie wyszedl ale:
Czarna kropka to srodek okregu
Kąt środkowy 2α wyznacza ten trójkąt zielony
Promień wynosi r
A, B to podstawa trojkata
Ten trojkat nie wychodzi poza okrag
Uwzględnij dane przedstawione na rysunku i oblicz długość cięciwy AB.
Troche mi rysunek nie wyszedl ale:
Czarna kropka to srodek okregu
Kąt środkowy 2α wyznacza ten trójkąt zielony
Promień wynosi r
A, B to podstawa trojkata
Ten trojkat nie wychodzi poza okrag

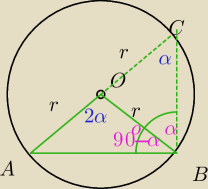 α i 2α kąty wpisany i środkowy oparte na tym samym łuku AB.
Jeśli nie miałe/aś tego twierdzenia, to obliczasz najpierw kąt 90o−α, potem z trójkąta
równoramiennego α.
α i 2α kąty wpisany i środkowy oparte na tym samym łuku AB.
Jeśli nie miałe/aś tego twierdzenia, to obliczasz najpierw kąt 90o−α, potem z trójkąta
równoramiennego α.
| |AB| | ||
w trójkącie prostokątnym ABC: | = sin α | |
| 2r |