Geometria Aga: W trójkąt prostokątny ABC o kącie prostym przy wierzchołku B, wpisano okrąg. Niech D oznacza punkt, w którym ten okrąg jest styczny do przeciwprostokątnej. Wykaż, że AB*BC=2*AD*DC Bardzo proszę o pomoc.

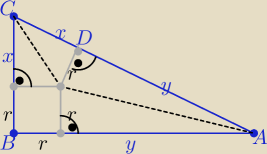
Eta: Najpierw wykazujemy ,że P(ABC)=x*y

	(r+x)*(r+y)
P(ABC)=P=		⇒ 2P= r2+rx+ry+xy
	2

i P= r²+rx+ry to: 2P=P+xy ⇒ P=x*y = |AD|*|DC|

	|AB|*|BC|
i P=
	2

	|AB|*|BC|
to		=|AD|*|DC| ⇒ |AB|*|BC|=2|AD|*|DC|
	2

==================== c.n.w.

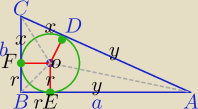
Mila: 1) a=r+y b=r+x |EA|=|AD=y| i |CD|=|CF|=x

	1
2) PΔABC=		a*b
	2

	1		1		1		1
PΔABC=r2+		y*r+		y*r+		(x+y)*r+		x*r=
	2		2		2		2

=r²+(x+y)*r

	1
r2+(x+y)*r=		a*b
	2

3) a*b=(x+r)*(y+r) a*b=x*y+xr+yr+r²⇔ a*b=x*y+ [(x+y)*r+r²]

	1
a*b=x*y+		a*b
	2

1
	a*b=x*y
2

a*b=2*x*y =========== cnw

Eta: