 11
Komnaty 2−kwadratowe o obwodzie 6 odpadają, bo nie ma innych komnat o obwodzie 6 oraz
35=17*2+1, więc zostałaby komnata 1−kwadratowa o obwodzie 4 (o ile w ogóle pionową i poziomą
orientację komnat 2−kwadratowych można traktować jako różne kształty).
Więc patrzymy na komnaty 3−kwadratowe, każda ma obwód równy 8 (bez względu na kształt), ale 35
nie jest podzielne przez 3, więc z samych 3−kwadratowych nie da rady. Jednak jest jeszcze
pokój 4−kwadratowy o obwodzie 8 (kwadrat 2x2). Równanie 3x+4y=35 już ma rozwiązania naturalne:
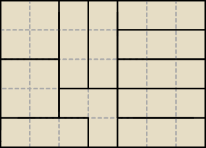
x=9, y=2 lub x=5, y=5 lub x=1, y=8. Wybieramy to o największej sumie x+y (liczbie komnat),
próbujemy narysować i przykładowo masz to co wyżej.
Więcej się nie da na podanych warunkach, bo wszystkie komnaty 2−kwadratowe i 3−kwadratowe
11
Komnaty 2−kwadratowe o obwodzie 6 odpadają, bo nie ma innych komnat o obwodzie 6 oraz
35=17*2+1, więc zostałaby komnata 1−kwadratowa o obwodzie 4 (o ile w ogóle pionową i poziomą
orientację komnat 2−kwadratowych można traktować jako różne kształty).
Więc patrzymy na komnaty 3−kwadratowe, każda ma obwód równy 8 (bez względu na kształt), ale 35
nie jest podzielne przez 3, więc z samych 3−kwadratowych nie da rady. Jednak jest jeszcze
pokój 4−kwadratowy o obwodzie 8 (kwadrat 2x2). Równanie 3x+4y=35 już ma rozwiązania naturalne:
x=9, y=2 lub x=5, y=5 lub x=1, y=8. Wybieramy to o największej sumie x+y (liczbie komnat),
próbujemy narysować i przykładowo masz to co wyżej.
Więcej się nie da na podanych warunkach, bo wszystkie komnaty 2−kwadratowe i 3−kwadratowe
| 35 | ||
rozpatrzyliśmy oraz | <11. | |
| 4 |