 Czyli np. pierwszy przypadek x>=0, y>=0, wtedy y<−x+3, więc rysuję i zamalowuję tylko ten
trójkąt, gdyż muszę patrzeć na dziedzinę, tak? I odpowiednio 4 razy dla innych przypadków.
Zgadza się?
Czyli np. pierwszy przypadek x>=0, y>=0, wtedy y<−x+3, więc rysuję i zamalowuję tylko ten
trójkąt, gdyż muszę patrzeć na dziedzinę, tak? I odpowiednio 4 razy dla innych przypadków.
Zgadza się?
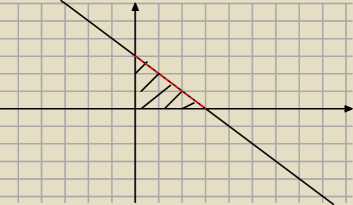 Dla 1 przypadku zamalowujesz tak jak piszsesz bez linii y=−x+3
Tutaj dziedzina to chyba nie ma nic wspolnego z tym
Dla 1 przypadku zamalowujesz tak jak piszsesz bez linii y=−x+3
Tutaj dziedzina to chyba nie ma nic wspolnego z tym

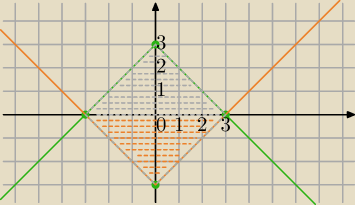 |x| + |y|<3
|y|<3−|x|
1) y≥0 ( punkty nad osią OX)
|y|=y
y<3−|x| punkty pod wykresem funkcji: y=3−|x| i nad osią OX
2) y<0
|y|=−y
−y<3−|x|⇔
y>|x|−3 punkty nad wykresem funkcji: y=3−|x| i pod osią OX
|x| + |y|<3
|y|<3−|x|
1) y≥0 ( punkty nad osią OX)
|y|=y
y<3−|x| punkty pod wykresem funkcji: y=3−|x| i nad osią OX
2) y<0
|y|=−y
−y<3−|x|⇔
y>|x|−3 punkty nad wykresem funkcji: y=3−|x| i pod osią OX
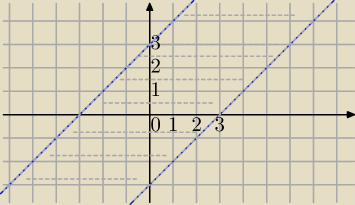 1)
|x−y|<3
2|x| − 3|y| > 6
|x−y|<3⇔
−3<x−y<3 rozpiszemy na dwie nierówności
x−y>−3 i x−y<3
x+3>y i x−3<y⇔
y<x+3 i y>x−3 obszar między prostymi y=x−3 i y=x+3
2)
2|x|−3|y|>6
a)
y≥0
2|x|−y>6
2|x|−6>y
y<2|x|−6
to narysuję w następnym wątku.
1)
|x−y|<3
2|x| − 3|y| > 6
|x−y|<3⇔
−3<x−y<3 rozpiszemy na dwie nierówności
x−y>−3 i x−y<3
x+3>y i x−3<y⇔
y<x+3 i y>x−3 obszar między prostymi y=x−3 i y=x+3
2)
2|x|−3|y|>6
a)
y≥0
2|x|−y>6
2|x|−6>y
y<2|x|−6
to narysuję w następnym wątku.
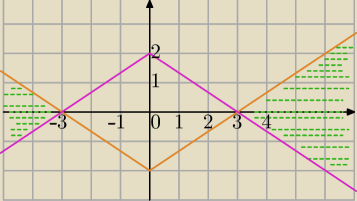 2)
2|x|−3|y|>6
a)
y≥0
|y|=y
2|x|−3y>6
2|x|−6>3y
2)
2|x|−3|y|>6
a)
y≥0
|y|=y
2|x|−3y>6
2|x|−6>3y
| 2 | 2 | |||
y< | |x|−2 obszar poniżej wykresu f. y= | |x|−2 | ||
| 3 | 3 |
| 2 | ||
y>− | |x|+2 obszar powyżej wykresu | |
| 3 |