Parametr Lila: Dla jakich wartości parametru k równanie x²−|4x−4|=(3−2k)/5 ma tyle samo rozwiązań dodatnich co ujemnych? Wykres mam I wiem o co chodzi ale dlaczego za przedział jest uznany − 4<(3−2k)/5<0 Tylko tego nie rozumiem. A dlaczego nie od − 8

iteRacj@: ponieważ dla przedziału (−8,−4) są dwa rozwiązania ujemne

Lila: No ale w poleceniu jest ze maja być ujemne

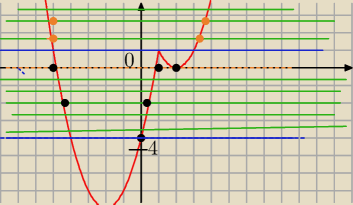
Krzysiek60: Przeczytaj jeszcze raz polecenie ma byc tyle samo rozwiazan dodatnich co ujemnych od y∊(−8,−4) masz dwa rozwiazania ujemne wiec odpada dla y=−4 masz jedno ujemne i 0 tez odpada bo ma byc dodatnie dla y∊(−4,0) masz jedno rozwiazanie ujemne i jedno dodatnie (bingo dla y∊<0,1> masz jedno ujemne i 2 dodatnie (odpada dla y∊(1,∞) masz jedno dodatnie i jedno ujemne (bingo

iteRacj@: Czy zgodzicie się, że jeszcze dla y∊(−∞,−8) jest samo rozwiązań dodatnich co ujemnych : )

Lila: Dziękuję bardzo

PW: Właśnie, właśnie. iteracj@ słusznie zwraca uwagę, że zadanie jest "paskudne". Zero rozwiązań dodatnich i zero rozwiązań ujemnych może być uznane za "tyle samo rozwiązań dodatnich i ujemnych". Ciekawe jaka jest odpowiedź w książce. Autor mógł uznać, że rozwiązanie to jest "coś co istnieje", a więc nieistniejące rozwiazania równania nie spełniają warunków zadania. Przychylam się do takiego rozumienia zadania.