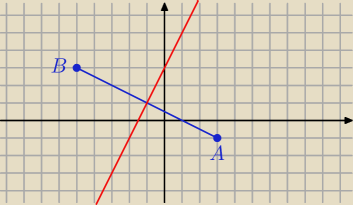
Jak to obliczyć? Alfred: Punkty A (3, −1) i B (−5,3) są wierzchołkami trójkąta równoramiennego ABC, w którym |AC|=|BC|. Wyznacz równanie prostej zawierającej wysokość prowadzoną z wierzchołka C. Proszę pomocy

the foxi: punkty A i B tworzą podstawę trójkąta wysokość trójkąta równoramiennego przechodzi przez środek podstawy

	3−(−1)		1
współczynnik kierunkowy prostej zawierającej punkty A i B: aAB=		=−
	−5−3		2

więc współcznnik kierunkowy prostej zawierającej wysokość to a_h=2 zatem prosta zawierająca wysokość jest postaci y=2x+b oblicz współrzędne środka odcinka AB i podstaw je do równania prostej, by wyliczyć B

Krzysiek60: W trojkacie rownoramiennym wysokosc jest tez symetralna podstawy Symetralna to zbior punktow odleglych jednakowo od koncow odcinka A=(3−1) B=(−5,3) Wobec tego √(x−3)²+(y+1)²= √(x+5)²+(y−3)² (podniszse obie strony do potgi drugiej (x−3)²+(y+1)²= (x+5)²+(y−3)² x²−6x+9+y²+2y+1= x²+10x+25+y²−6y+9 −6x+2y+10−10x+6y−34=0 −16x+8y−24=0 (dziele przez 8 −2x+y−3=0 (postac ogolna y=2x+3 postac kierunkowa

Janek191:

the foxi: Krzysiek ciekawy sposób, warto zapamiętać

Krzysiek60: Mila i PW tez o nim pisali mam problem z Firewoksem . Nie zmniejsza mi obrazu gdy mam pelny ekram i daje na to srodkowe okienko (ledwo obraz drgnie przeszkadza mi to bo nie moge dac zadanka na pulpit . Internet Explorer dziala