Zaznacz zbiór w układzie współrzędnych. Karolina: W prostokątnym układzie współrzędnych XOY zaznacz zbiór: A = {(x,y): x in\ R i y in\ R i 4^{log₂₅(x−2y)}+9^log₃(2x+y) \< 25^log₅√5 } Oblicz pole i długość brzegu figury A

Adamm: znak "∊" masz na górze klikasz, i wyskakuje

Adamm: Jesteś pewna że tam jest 4^{log₂₅(x−2y)} ? Bo to tylko komplikuje sprawy

Karolina: U mnie te znaki nie były widoczne, teraz otworzyłam stronę w innej przeglądarce i już je mam. dzięki! oczywiście, że zrobiłam tam błąd... tam jest 2 w podstawie. umiem to sprowadzić do jakiejś sensowniejszej nierówności, wiem że podstawy się "skracają" itd, ale co dalej z tym zrobić? Chyba jednak pora założyć konto, wtedy będę mogła edytować?

Mila: czy x,y∊R? Czy nierówność ostra? 4^{log₂(2−y)}+9^log₃(2x+y)<25^log₅(√5) taki zapis?

iteRacj@: chyba tak Milu 4^{log₂(x−2y)}+9^log₃(2x+y) < 25^log₅√5 zał. x−2y>0 , 2x+y>0 i wtedy (2^{log₂(x−2y)})²+(3^log₃(2x+y))² < (5^log₅√5)²

iteRacj@: już widzę w poleceniu, dlaczego podejrzewasz nieostrą nierówność : )

Karolina: A = {(x,y): x∊R i y∊R i 4^{log₅(x−2y)}+9^log₃(2x+y) ≤ 25^log₅√5 } Wybaczcie to zamieszanie, teraz kiedy już widzę te znaki to myślę że będzie łatwiej naprawdę nie wiem o co chodzi. na chromie po prostu je ucięło, na firefox wszystko ok..

Mila: Ja źle przepisałam pierwszą liczbę logarytmowaną. D: x−2y>0 i 2x+y>0

	1
y<		x i y>−2x
	2

2^{log₂(x−2y)2}+3^{log₃(2x+y)2}<5^{log₅(√5)2} (x−2y)²+(2x+y)²<5⇔ x²+y²<1 i (x,y)∊D

Karolina: iteRacj@ Do tego już niestety doszłam, poprzeliczałam na kilka sposobów w nadziei że coś się skróci ale nawet z prostą formą nie mam pojęcia co zrobić dalej... nie rozumiem w ogóle jak mam zaznaczyć taki wzór w układzie współrzędnych

iteRacj@: już Mila to wyjaśniła

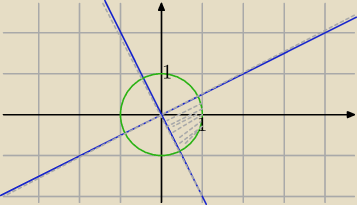
Mila:

	1
Proste y=		x i y=−2x są prostopadłe.
	2

Masz ćwiartkę koła.

Mila: Przepraszam, masz dobrze, ja stosuję inną metodę, Twój zapis dobry

iteRacj@: uff : )