matematykaszkolna.pl
Rozwiąż nierówność(nierówności wykładnicze): Sawyer: 5*42x−3*52x≥2*20x
6 paź 17:08
Jerzy: Wskazówka: 20x = 4x*5X Potem podziel obustronnie przez ten iloczyn.
6 paź 17:26
Sawyer: Wychodzi 5*(4/5)x−3*(5/4)x≥2 co dalej ? Wynik to (−∞,0》
6 paź 17:57
Mila: Podstawienie :
 4 
(
)x=t
 5 
 5 1 
(
)x=
, t>0
 4 t 
6 paź 18:04
Sawyer: Teraz jest dobrze, dziękuje serdecznie
6 paź 18:15
Pompka : Pani Milu .Prosze rozwiazac ten przyklad caly .dziekuje
6 paź 18:30
Maciess: Rozwiązuje
6 paź 18:40
Mila: emotka
6 paź 18:41
Maciess: rysunek
5*42x 3*52x 
−
≥2
5x*4x 5x*4x 
 4x 5x 
5*
−3*
≥2
 5x 4x 
 4 
t=(
)x t>0
 5 
 1 
5t−3*
≥2 /*t
 t 
5t2−2t−3≥0
 3 
t1=−
t2=1
 5 
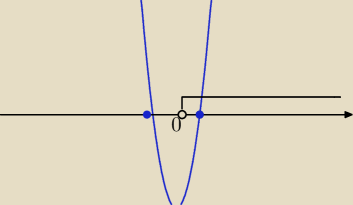
t∊<1,+∞) Czyli musimy rozwiązać t≥1 i tu wracamy do naszej podstawionej wartosci
 4 
(
)x≥1
 5 
 4 4 
(
)x≥
0
 5 5 
x≤0
6 paź 18:48
Pompka : Ok . dzieki .
6 paź 18:50
Maciess: Przedostatnia linijka, ułamek w nawias bo to by była bzdura
6 paź 18:52
Mila: Dobrze. Może jeszcze dodać:
 3 
(t+
)*(t−1)>0⇔
 5 
 3 
t−1>0 ponieważ: t+
>0 dla t>0
 5 
stąd t>1 i dalej tak ,jak napisał Maciess.
6 paź 20:06