| 3x | ||
f(x)= | ||
| 2x−5 |
| 3x | ||
Z tego co rozumiem to dziedziną funkcji są liczby rzeczywiste; piszemy y= | i mnożymy | |
| 2x−5 |
| 1 | ||
f−1(x) = | +5/2 | |
| x−3/2 |
| a | ||
f−1(x) = | +5/2 | |
| x−3/2 |
| 2 | ||
f(0) = 0 ⇒ f−1(0)=0 ⇒ − | a+5/2=0 ⇒ a=15/4 | |
| 3 |
| 15/4 | ||
f−1(x) = | +5/2 | |
| x−3/2 |
| 5y | ||
x = | ||
| 2y−3 |
| 5x | ||
f−1(x) = | ||
| 2x−3 |
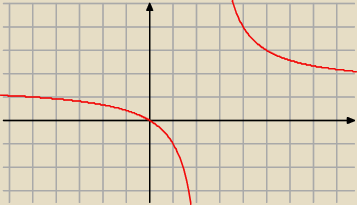 Nie wolno rzucać się od razu na wyznaczanie funkcji odwrotnej, bo nie wiadomo czy coś takiego w
ogóle istnieje.
Można mówić o funkcji odwrotnej do f, jeżeli f jest różnowartościowa. Jak widać na rysunku −
tak jest. Adamm o tym wie, ale nic nie napisał, zakłada że wiesz jak wygląda wykres
funkcji homograficznej i znasz jej własności. Zakłada również wiedzę, że funkcja odwrotna do
homograficznej jest też homograficzna. Dlatego pisze o jej asymptotach. To jest chyba za
trudny sposób myślenia dla przeciętnego ucznia.
Nie wolno rzucać się od razu na wyznaczanie funkcji odwrotnej, bo nie wiadomo czy coś takiego w
ogóle istnieje.
Można mówić o funkcji odwrotnej do f, jeżeli f jest różnowartościowa. Jak widać na rysunku −
tak jest. Adamm o tym wie, ale nic nie napisał, zakłada że wiesz jak wygląda wykres
funkcji homograficznej i znasz jej własności. Zakłada również wiedzę, że funkcja odwrotna do
homograficznej jest też homograficzna. Dlatego pisze o jej asymptotach. To jest chyba za
trudny sposób myślenia dla przeciętnego ucznia.