Wykaż że funkcja ma minimum jedno miejsce zerowe
mxx: Wykaż że funkcja ma minimum jedno miejsce zerowe f(x)=1/2−2+sinx
6 paź 13:54
Jerzy:
| | 1 | | 3 | |
f(x) = 0 ⇔ |
| − 2 + sinx = 0 ⇔ sinx = |
| ( brak miejsc zerowych ) |
| | 2 | | 2 | |
6 paź 13:58
mxx: Wkradła się mała pomyłka miało być
Wykaż że funkcja ma minimum jedno miejsce zerowe f(x)=1/2x−2+sinx
6 paź 14:01
the foxi:
funkcja jest ciągła w zbiorze liczb rzeczywistych
f(5)≈2.5−2−0.96<0
f(6.28)≈f(2π)≈3.14−2+0≈1.14
korzystając z własności Darboux funkcja f(x) ma w przedziale x∊(5;2π) co najmniej jedno miejsce
zerowe
6 paź 14:05
Janek191:
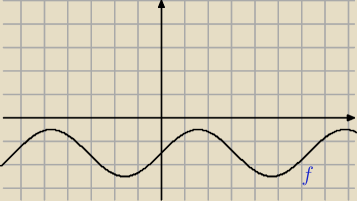
6 paź 14:09
Janek191:
Pewnie źle przepisano treść zadania ?

6 paź 14:11
6 paź 14:56

