Nierówność trygonometryczna
Mateusz: Hejka, proszę o pomoc z równaniem
cos2x(1−sinx)>=0
Jak myślicie? Rozważyć tutaj przedziały, czy zrobić to w jakis inny sposób?
4 paź 20:15
a7: (1−2sin2x)(1−sinx)>=0
sinx=t i t należy od − 1 do 1
(1−2t2)(1−t)>=0
t=1/4 lub t=−1/4 lub t=1
rysujemy oś, sprawdzamy jaki znak przyjmuje nierówność w przedziałach i mamy odpowiedź do
zadania
(?)
4 paź 20:54
Mateusz: | | 1 | |
wyszło mi, ze sinx należy < |
| ,1> |
| | 4 | |
4 paź 20:59
a7: jeśli t= 0 to nierówność też jest większa równa zero (?)
4 paź 21:01
Mateusz: nie za bardzo rozumiem co masz na myśli?
4 paź 21:04
a7:
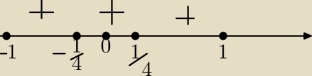
4 paź 21:05
a7: ?
4 paź 21:05
a7: nie wiem czy dobrze myślę, ale mi wychodzi, że dla każdego t należącego od −1 do 1 nierówność
jest większa równa zero
czyli
x∊R
(?)
4 paź 21:07
Mateusz: Już nie ważne, poradziłem sobie

4 paź 21:09
Mateusz: źle rozwiązaliśmy "t"
| | √2 | | √2 | |
t wynosi 1, − |
| oraz |
| . t3 ma współczynnik dodatni, rysujemy wykres od góry |
| | 2 | | 2 | |
prawej strony i przecinamy trzy razy. Po uwzględnieniu dziedziny wychodzi, że x nalezy od
−pi/4 do pi/4
4 paź 21:13
a7: tzn. faktycznie źle wyznaczyłam t , natomiast sprawdziłabym czy znak gdzieś się nie odbija i
nie jest nadal dodatni biorąc przykładową liczbę z danego przedziału i wstawiając ją do
nierówności w której jest t.
4 paź 21:27
Mila:
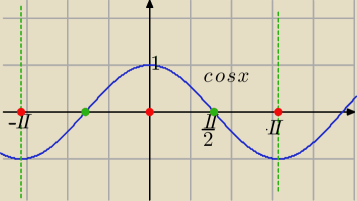
1−sinx≥0 dla x∊R
i
cos(2x)≥0
| | π | | π | |
− |
| +2kπ≤2x≤ |
| +2kπ /:2 |
| | 2 | | 2 | |
| | π | | π | |
− |
| +kπ≤x≤ |
| +2kπ i x∊{kπ} |
| | 4 | | 4 | |
4 paź 22:30


 1−sinx≥0 dla x∊R
i
cos(2x)≥0
1−sinx≥0 dla x∊R
i
cos(2x)≥0