graniastlup humanista: W graniastosłupie prawidłowym trójkątny krawędź postawy to a. Odcinek łączący środki symetrii dwóch ścian bocznych widac pod kątem α ze środka ciężkości podstawy. Oblicz objętość graniastosłupa.

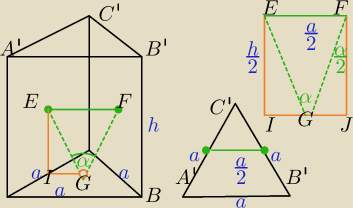
iteRacj@: E,F − środki symetrii ścian bocznych G − środek ciężkości podstawy

	1
|EF|=		a
	2

	1
|EI|=		h
	2

	α
<GFJ=
	2

	α		GJ		a   4		a		a
tg		=		=		=		⇒ h=
	2		FJ		h   2		2h		α   2tg   2

P_p − pole podstawy

	a2√3
Pp =
	4

	a2√3		a
V=		*
	4		α   2tg   2

humanista:

	3a3tg(90−α2)
czy jeżeli objętość mi wyszła		to jest to zły wynik?
	12

Mila: Sprawdzę swoje obliczenia, a Ty sprawdź swoje

iteRacj@: Twój wynik nie jest poprawny.

iteRacj@: Mila napisz jak sprawdzisz, bo obie mamy ten sam wynik

Mila: Ja mam błąd Zaraz policzę na nowo.

Mila: Błędnie ustaliłam wysokość. ( Rysunek !) Już piszę.

Mila:

	1
|PQ|=		a
	2

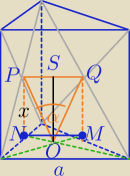
1) W ΔPSO:

	α		PS		α		1   a 4		a
sin		=		⇔sin		=		⇔ |OP|=
	2		OP		2		OP		α   4sin   2

	1		a√3
2) W PNO: |NO|=		*
	3		2

	a√3
|OP|2=x2+(		)2
	6

Stąd

	a2*(3−4sin2(α/2))
x2=
	48sin2(α/2)

	a*√3−4sin2(α/2)
x=
	4√3sin(α/2

	a*√3−4sin2(α/2)
H=
	2√3sin(α/2)

	a2√3		a*√3−4sin2(α/2)
V=		*
	4		2√3sin(α/2)

	a3√3−4sin2(α/2)
V=
	8sin(α/2)

=======================

Mila: iteRacjo OS nie leży w płaszczyźnie MNPQ. Stąd miałam błąd. Humanisto, napisz z jakiego trójkąta wyznaczyłeś wysokość.

xn:

iteRacj@: Taki właśnie błąd popełniłam i nie umiałabym tego zobaczyć.

Mila: To "dokształciłyśmy" się, a humanista nie jest zainteresowany. Pozdrawiam

iteRacj@: naprawdę dużo można się w taki sposób nauczyć, dziękuję za wyjaśnienie