Ostroslup kiki: Przekrój ostroslup prawidłowego trójkątnego płaszczyzna zawierającą krawędź podstawy i środek wysokości ostroslupa ma pole 2√6. Płaszczyzna przekroju jest nachylenia do podstawy pod kątem 45°. Wynika stąd że pole podstawy jest równe? Prawidłowa odpowiedź do 4√3

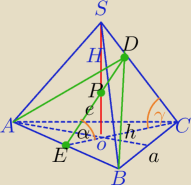
Mila: α=45^o, h− wysokość podstawy, |ED|=e− wysokość ΔABD

	1		1
1) |EO|=		H i |EO|=		h⇔
	2		3

	2
H=		h⇔ΔSOC− Δprostokatny równoramienny, ∡γ=45o
	3

W takim razie ΔDEC jest też Δrównoramiennym i prostokątnym (90,45,45) |ED|=|DC| h²=2e²

	h
e=
	√2

	1
2) PABD=2√6⇔ 2√6=		a*e
	2

	1		h		1
2√6=		*a*		/*√2 ⇔2√12=		a*h
	2		√2		2

	1
4√3=		a*h
	2

P_ΔABC=4√3 =============

Krzysiek60: Dobry wieczor Milu mam pytanie . Skoro przekroj zawiera srodek wysokosci ostroslupa to dlaczego jedziesz z nim na krawedz ostroslupa ?

Mila: Tak przecięłam ciastko piramidkę

Krzysiek60: Milu tez mialem lekki wypadek w pracy we wrzesniu . stanalem na gwozdzia . Teraz zalapalem przeziebienie . Pracowalem na przeciagu . mam tez pytania do zadania

	2
Dalczego H=		h ? , Dlaczego γ= 45o ? Mozesz wyjasnic ?
	3

Krzysiek60:

	1
Plus do tego powinno byc |PO|=		H no ale to wiadomo
	2

Mila: Tak. Rozwiązywałam wcześniej inną metodą, potem usuwałam pewne wpisy i przy okazji to co napisałeś

Mila: Ad. 22:21 1) ΔEOP− Δprostokątny równoramienny.

	1
|EO|=		h=|OP|
	3

	1		2
|OP|=		H z treści zad.⇒H=		h
	2		3

================================ 2) |SO|=|OC|⇔ΔSOC− Δprostokatny równoramienny stąd γ=45^o. ===============================================