Geometria analityczna - okrąg i środki jego cięciw Janek: Cześć, mam problem z tym zadanie i nie wiem jak wystartować: Z początku układu współrzędnych poprowadzono cięciwy okręgu x² + y² = 2x . Znajdź miejsce geometryczne środków tych cięciw.

Blee: 1) wyznaczasz środek i promień okręgu 2) wyznaczasz STYCZNE do tegoż okręgu przechodzące przez początek układu współrzędnych 3) w tym momencie masz trzy punkty które będą tworzyć zbiór rozwiązań (z czego dwa ostatecznie do tego zbioru nie będą należeć) są nimi: oba punkty styczności (które właśnie należeć nie będą) oraz środek okręgu 4) możesz wyznaczyć jeszcze parę punktów jeżeli nie masz pewności co do tego jak będzie wygląda zbiór rozwiązań

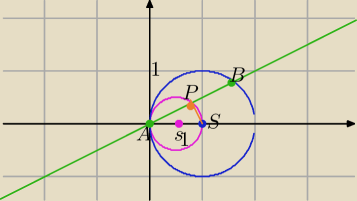
Mila: x² + y² = 2x x²−2x+y²=0 (x−1)²−1+y²=0 (x−1)²+y²=1 okrąg o środku S=(1,0) i r=1 P(x,y) − środek cięciwy AB,S− środek okręgu PS⊥AB ΔAPS− Δprostokątny 1²=|AP|²+|PS|² 1²=x²+y²+(1−x)²+(0−y)² 1=x²+y²+1−2x+x²+y² 2x²+2y²−2x=0 x²+y²−x=0

	1		1
(x−		)2+y2=(		)2
	2		2

	1		1
okrąg o środku S1=(		,0) i r'=
	2		2

=========================

Janek: Dziękuję Wam bardzo!

Mila: