Pomocy
Dominik: Za pomocą tabeli prawdy udowodnij wszystkie prawa rachunku zdań
Prawo przemienności
p∨q⇔q∨p
p∧q⇔p∧q
Robię tabelkę
p q p∨q q∨p p∨q⇔q∨p p q p∧q p∧q p∧q⇔p∧q
0 0 0 0 0 0 0 0 0 0
1 0 1 1 1 1 0 0 0 0
0 1 1 1 1 0 1 0 0 0
1 1 1 1 1 1 1 1 1 1
Dobrze myślę? Jeżeli nie to gdzie jest błąd?
2 paź 20:20
Adam: Jeśli a jest fałszywe i b jest fałszywe to a⇔b jest prawdziwe
2 paź 20:25
Adam: W związku z tym w ostatnich kolumnach wszędzie są 1, więc podane zdania są zawsze prawdziwe
(tautologia).
2 paź 20:28
Blee:
0 ∧ 0 −> 1
i gdzie tutaj jest przemienność (w drugim)
2 paź 20:39
Blee:
tfu 0 ⇔ 0 −> 1 miało być

2 paź 20:40
Dominik: A pomożesz mi z kolejnym zadaniem?
2 paź 20:42
Dominik: Prawo łączności
(p∨q)∨r⇔p∨(q∨r)⇔p∨q∨r
Jak to zapisać w tabelce?
2 paź 20:48
Blee:
zależy jakim
2 paź 20:48
Blee:
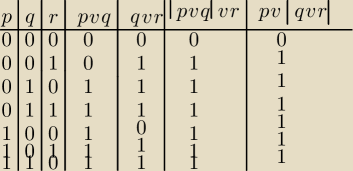
i jeszcze nie zmieściło mi się 1;1;1 (dla p;q;r)
no i samemu robisz dla p v q v r
2 paź 20:54
Dominik: Czyli ta tabelka nie udowodni prawdziwości twierdzenia?
2 paź 21:12
Dominik: I jeszcze jedno pytanie, dlaczego (pvq) i (qvr) są w nawiasach?
2 paź 21:14
Blee:
jak nie udowodni jak udowodni
bo MASZ TAK PODANE (patrz − kolejność działań

)
2 paź 21:32
Blee:
tylko musisz tą tabelkę DOKOŃCZYĆ

2 paź 21:32
Dominik: No nawet jak dokończę tabelkę to w pierwszym wierszy (0,0,0) dla pvqvr będzie 0 a żeby był
dowód, to cała kolumna musi być prawdziwa czyli 1?
2 paź 21:38
Dominik: Chyba, że tu też chodzi o tautologię?
2 paź 21:41
Blee:
0 ⇔ 0 −> 1 już Ci to pisaliśmy wcześniej

2 paź 21:43
Blee:
to nie p v (q v r) ma dać same jedynki tylko
p v (q v r) ma mieć taki sam układ 0 i 1 co pozostałe

2 paź 21:44
Dominik: @Blee OK 0⇔0 → 1 To zrozumiałem
Nie rozumiem nadal tego
cytat
"p v (q v r) ma mieć taki sam układ 0 i 1 co pozostałe "
2 paź 22:11
Blee:
jeżeli zdanie a i zdanie b będzie miał 'ten sam układ 0 i 1'
to przy a ⇔ b będzie tylko taka sytuacj: 0 ⇔ 0 lub 1 ⇔ 1 (taki sam układ 0 i 1)
2 paź 22:19
Blee:
patrz tabelka i (p v q) v r oraz p v (q v r)
mają taki sam 'układ 0 i 1' więc ( (p v q) v r ) ⇔ ( p v (q v r) ) wyjdzie jako tautologia
(same 1)
2 paź 22:20
Dominik: ok chyba rozumiem, dziękuję

2 paź 23:12

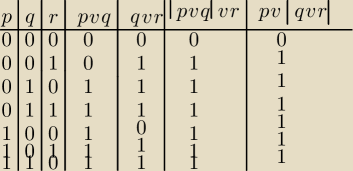 i jeszcze nie zmieściło mi się 1;1;1 (dla p;q;r)
no i samemu robisz dla p v q v r
i jeszcze nie zmieściło mi się 1;1;1 (dla p;q;r)
no i samemu robisz dla p v q v r
 )
)



