Rozwiąż trójkąt przy pomocy twierdzenia sinusów. Jakub: Witam. Do rozwiązania mam trójkąt o danych: a=3, b=6, α=40 (stopni). Dochodzę do punktu w którym sin β = 1,28, a z tego co wiem jest to niemożliwe. Serdecznie proszę o pomoc!

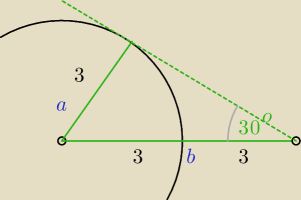
ite: kąt naprzeciwko boku a może mieć 30^o

ite: *co najwyżej 30^o

Jakub: Czyli jak rozwiązanie jest niemożliwe?

ite: według mnie nie zgadzają się dane w tym zadaniu, zbudowanie trójkąta o takich bokach i kącie α jest niemożliwe

Adam: Jeśli nie jest powiedziane inaczej to zawsze zakłada się, że α jest na przeciwko a, β jest na przeciwko b i γ na przeciwko c. Skąd 30^o? W zadaniu jest 40^o.

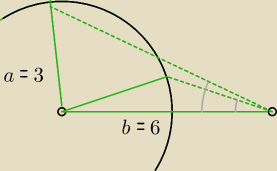
ite: Tak właśnie jest u mnie: naprzeciwko boku a=3 jest kąt α (kolor szary). Na rysunku z 14:26 narysowałam największy możliwy kąt α = 30^o, jaki można otrzymać przy założeniu, że α jest na przeciwko boku a=3, a bok b=6. Rysunek powyżej ilustruje, że pozostałe możliwe kąty będą mniejsze niż 30^o. Nie da się zbudować trójkąta o podanych bokach i kącie α>30^o czyli α≠40^o.

Adam: A sorki, źle przeczytałem. Jakub masz dobrze. Z twierdzenia sinusów wynika, że sinβ≈1,28 a z tego wynika, że trójkąt o zadanych bokach i kącie nie istnieje.

Jakub: Serdecznie dziękuję za odpowiedzi, moje wątpliwości zostały rozwiane