Czy taka ścieżka przekształceń funkcji jest poprawna? Meumann: Mamy f(x), a g(x)=f(2−x). Zatem, f(x)−>symetria na osi OY = f(−x) −> przesunięcie o wektor [−2,0] = f(2−x)=g(x) Czy jest to poprawny tok przekształceń, czy powinno być na odwrót? Czy jest jakaś reguła?

ICSP: o wektor [2 , 0] , (2 − x) = − (x − 2)

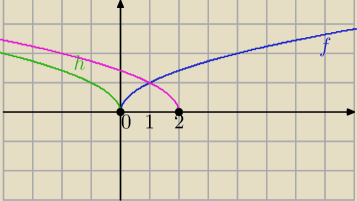
Mila: Przekształcanie wykresów funkcji: 1) f(x−a) f(x)→T_[a,0]⇒otrzymujemy wykres y=f(x−a) 2) f(a−x) I sposób: ( najpierw przesunięcie (translacja) f(x)→T_[−a,0]⇒otrzymujesz wykres y=f(x+a)→S_OY⇒ wykres y=f(−x−a) Twoje zadanie : f(2−x) 1) f(x)→T_[−2,0]⇒y=f(x+2)→S_OY⇒y=f(−x+2) II sposób ( najpierw symetria względem OY) f(a−x) f(x)→S_OY⇒y=f(−x)→T_[a,0]⇒y=f(−x+a) Przykład : f(x)=√x Chcemy otrzymać wykres g(x)=f(2−x)=√2−x −x+2≥0⇔−x≥−2⇔x≤2 II sposób 1) y=√x→S_OY⇔h(x)=√−x→T_[2,0]⇒f(x)=√−x+2

Eta: Ja to przekształcam tak: (jak podałaś w II sposobie) y=f [−(x−2)] najpierw symetria S_0y i przesunięcie (translacja ) w prawo o 2 jednostki na jedno wychodzi

Mila: Dziękuję, ja też wolę II sposób.