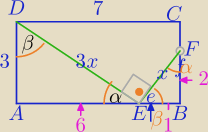
Dwa sąsiednie boki prostokąta. oblicz pole DEFC. hitman69: Dwa sąsiednie boki prostokąta ABCD mają długość: AB = 7 BC =3 Z punktu D poprowadzona prostą która przeciela bok AB w punkcie E, a nastepnie prostą prostopadłą do preostej DE, która przechodzi przez punkt E i przecina bok BC w punkcie F (rysunek obok). Wiedząc ze DE = 3EF oblicz pole czworokąta DEFC. Protokąt po kolei jak wskazówki zegara ABCD, kąt prostu tam. na dole kąt E i na boku BC jest F

hitman69: bump

Mila: α+β=90^o α+e=90⇒e=β f=α

	3		EB
ΔDAE∼ΔEBF⇔		=		⇔|EB|=1
	3x		x

|AE|=7−1=6

6		FB
	=		⇔|FB|=2
3x		x

	1		1
PDEFC=7*3−(		*3*6+		*1*2)=
	2		2

=21−10=11 P_DEFC=11 ===========