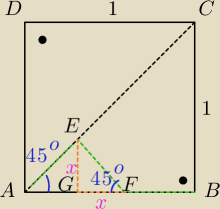
 |AB|=|BC|=1 oraz |AC|=√2
|AE|=|EF|=|FB| i |<EAG|=|<EFG|=45o ⇒ |EG|=|GF| = x
PCEFB=PABC−PAEF
obliczenie wielkości PABC nie stanowi problemu
teraz obliczenie PAEF=x2
w Δ EFG: x2+x2=|EF|2
|EF|=√2x
|AB|=2x+|EF|
2x+|EF|=1
2x+√2x=1
x(2+√2)=1 ← z tego wylicz x
dalej oblicz PAEF i na koniec szukane pole PCEFB
|AB|=|BC|=1 oraz |AC|=√2
|AE|=|EF|=|FB| i |<EAG|=|<EFG|=45o ⇒ |EG|=|GF| = x
PCEFB=PABC−PAEF
obliczenie wielkości PABC nie stanowi problemu
teraz obliczenie PAEF=x2
w Δ EFG: x2+x2=|EF|2
|EF|=√2x
|AB|=2x+|EF|
2x+|EF|=1
2x+√2x=1
x(2+√2)=1 ← z tego wylicz x
dalej oblicz PAEF i na koniec szukane pole PCEFB
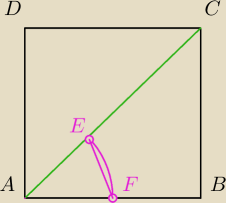 od połowy pola kwadratu odejmij pole ΔAEF
od połowy pola kwadratu odejmij pole ΔAEF