Pole trójkąta - styczne okręgów JanuszCebula: Dwа оkrеgi о рrоmiеniасh r i R, gdziе r < R, są stусznе zеwnеtrzniе. Wуznасz роlе trójkаtа оgrаniсzоnеgо iсh wsрólnуmi stусznуmi. Bardzo proszę o pomoc lub wskazówki

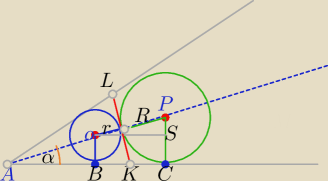
Mila: r<R BC⊥AP 1)ΔABO∼ΔOSP⇔ |PS|=R−r ∡POS=α

	PS		R−r
sinα=		⇔sinα=
	OP		r+R

a także

	r		r		R−r
sinα=		⇔		=		⇔
	AO		AO		r+R

	r2+r*R
|AO|=
	R−r

================= |OS|²=((r+R)²−(R−r)² |OS|=2√r*R

	|PS|		R−r
2)tgα=		⇔tgα=
	|OS|		2√r*R

3)M− środek odcinka KL W ΔAMK:

	MK
tgα=
	AM

R−r		MK
	=
2√r*R		AO+r

Oblicz MK 4)

	1
PΔAKL=		*2|MK|*|AM|
	2

JanuszCebula: Dziękuję <3

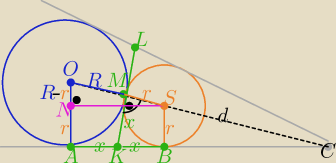
Eta: Z tw. Pitagorasa w ΔOSN : 2x=|NS|=√(R+r)²−(R−r) ⇒ x=√Rr Z podobieństwa trójkątów AOC i BSC

R		R+r+d		r(R+r)
	=		⇒ ... d=
r		d		R−r

to P(KLC) = x*(r+d) =............

	2Rr√Rr
P(KLC)=
	R−r

=====================

Eta: http://www.diament.agh.edu.pl/fileadmin/default/templates/css/j/diament/system/zadania/mat/2018/matematyka_i_2018_2019.pdf

Eta: Ładnie to tak?

PW: I tak nie poradzi sobie z pozostałymi, to było najłatwiejsze.

Benny: Drugie chyba jest łatwiejsze.