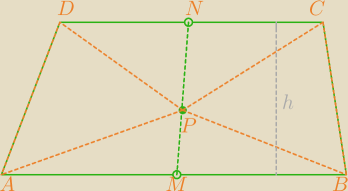
 1/ |DN|=|NC| i |AM|=MB| a trapezy AMND i NMBC taką same wysokości h ⇒ ich pola są równe.
PAMND=PNMBC
2/ Również wysokości trójkątów ΔDNP oraz ΔCNP są równe, a |DN|=|NC| ⇒ ich pola są równe.
PDNP=PCNP
3/ Wysokości trójkątów ΔAPM oraz ΔBMP są równe, a |AM|=MB| ⇒ ich pola są równe.
PAPM =PBMP
PAMND=PDNP+PAMP+PAPD
PNMBC=PCNP+PBMP+PBPC
PDNP+PAMP+PAPD=PCNP+PBMP+PBPC
PCNP+PBMP+PAPD=PCNP+PBMP+PBPC //−PCNP−PBMP
PAPD=PBPC
1/ |DN|=|NC| i |AM|=MB| a trapezy AMND i NMBC taką same wysokości h ⇒ ich pola są równe.
PAMND=PNMBC
2/ Również wysokości trójkątów ΔDNP oraz ΔCNP są równe, a |DN|=|NC| ⇒ ich pola są równe.
PDNP=PCNP
3/ Wysokości trójkątów ΔAPM oraz ΔBMP są równe, a |AM|=MB| ⇒ ich pola są równe.
PAPM =PBMP
PAMND=PDNP+PAMP+PAPD
PNMBC=PCNP+PBMP+PBPC
PDNP+PAMP+PAPD=PCNP+PBMP+PBPC
PCNP+PBMP+PAPD=PCNP+PBMP+PBPC //−PCNP−PBMP
PAPD=PBPC
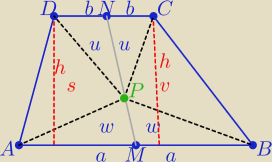 Każda środkowa trójkąta dzieli trójkąt na dwa trójkąty o równych polach
zatem :
P(AMP)=P(BMP)=w i P(DNP)=P(CNP)=u
Środkowa MN dzieli trapez na dwa trapezy o równych polach
zatem P(AMND)=P(BMNC) ⇒ u+w+s=u+w+v ⇒ s=v
c.n.w
Każda środkowa trójkąta dzieli trójkąt na dwa trójkąty o równych polach
zatem :
P(AMP)=P(BMP)=w i P(DNP)=P(CNP)=u
Środkowa MN dzieli trapez na dwa trapezy o równych polach
zatem P(AMND)=P(BMNC) ⇒ u+w+s=u+w+v ⇒ s=v
c.n.w
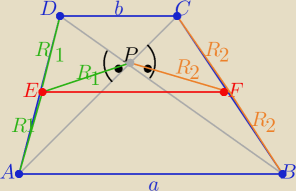 Można tak:
1/ rysunek...........
Można tak:
1/ rysunek...........
| a+b | ||
2/ dorysuj środkową EF , |EF|= | ||
| 2 |
| |AD| | |BC| | ||
+ | ≥|EF|⇒ |AD|+|BC|≥a+b | ||
| 2 | 2 |