wyznacz równania stycznych do okregu
ja: Wyznacz równania stycznych do okręgu o równaniu
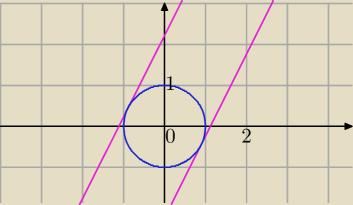
x2+y2=1
równoległych do prostych o równaniu y=2x+17
mam problem z tym zadaniem, wiem że promień =1 i styczne będą miały a=2
26 wrz 21:57
Mila:
s: y=2x+b⇔2x−y+b=0
| | |2*0−0+b| | |
d(s,O)=1= |
| |
| | √22+12 | |
|b|=
√5
b=
√5 lub b=−
√5
s:
y=2x+
√5
lub
s=2x−
√5
II sposób
x
2+(2x+b)
2=1 równanie ma jedno rozwiązanie⇔
Δ=0
26 wrz 22:12
the foxi:
styczne są postaci y=2x+b
i mają jeden punkt wspólny z okręgiem x
2+y
2=1, zatem:
x
2+(2x+b)
2−1=0 ← to równanie musi mieć jedno rozwiązanie, więc Δ=0
x
2+4x
2+4xb+b
2−1=0
5x
2+
4bx+
b2−1=0
(4b)
2−4*5(b
2−1)=0
...
i dalej, licz dla jakiego b delta jest równa 0
26 wrz 22:15
ja: bardzo dziękuję!
26 wrz 22:17
Mila:
26 wrz 22:51