proszę o rozwiązanie Anna: Ramię AD trapezu ABCD (w którym AB II CD) przedłużono do punktu. E takiego, że AE = 3 · AD. Punkt M leży na podstawie AB oraz MB = 4 · AM. odcinek ME przecina przekątną BD w punkcie P . Udowodnij że I BP I= 6 I PD I

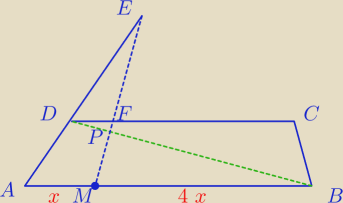
ite: |MB| = 4|AM|, |AE| = 3|AD| z tw.Talesa dla kąta <AEM

|ED|		|DF|		2		2
	=		=		⇒ |DF|=		x
|EA|		|AM|		3		3

z podobieństwa ΔDFP i ΔMBP

|DP|		|DF|		2   x 3		2   3		1
	=		=		=		=
|PB|		|MB|		4x		12   3		6

stąd IBPI= 6IPDI

Anna: dziękuję bardzo

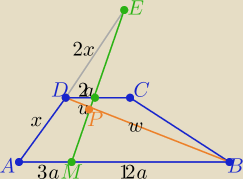
Eta: w/u=12a/2a ⇒ w/u=6 ⇒ |BP|=6|DP|