Zagwozdka z granicami
Pytajek :
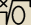
Witam, mam pytanie do czego dąży lim
x→∞(
√0)? (chodzi o pierwiastek stopnia x jak na
obrazku)
Wg. Wolfram Alpha (stronka do sprawdzania funkcji itp.) ta granica w minus nieskończoności
wynosi 1, a w plus nieskończoności wynosi 0.
https://www.wolframalpha.com/input/?i=%5Clim+_%7Bx%5Cto+%5Cinfty+%7D%5Cleft(%5Csqrt%5Bx%5D%7B0%7D%5Cright)
Pierwiastek można przekształcić w potęgę co da 0
1/x, więc gdy x dąży do nieskończoności
obojętnie której, to potęga powinna dążyć do 0, więc 0
0 wynosiło by 1, natomiast jest
zupełnie inaczej. Kompletnie tego nie rozumiem i byłbym wdzięczny za wytłumaczenie problemu.
26 wrz 01:28
PW: Tworzysz nieistniejące problemy. Co to miałoby być np. pierwiastek stopnia −3 z liczby 0?
26 wrz 06:24
Pytajek : Pierwiastek ujemnego stopnia dla zera jest niezdefiniowany, gdyż zakładając że ma się go
zamienić na potęgę wynikiem będzie dzielenie przez 0. Ja chciałbym się dowiedzieć czemu akurat
granica w plus nieskończoności wynosi 0 a nie 1.
26 wrz 08:52
jc:
01/x = 0, x>0. Dlatego 01/x →0 przy x→0.
Po prostu funkcja x→01/x, x>0, jest funkcją stałą: x→0.
Wygodnie przyjąć, że 00=1, ale wtedy funkcja t→0t, t≥0, nie będzie funkcją
ciągłą w punkcie zero.
26 wrz 09:51
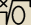 Witam, mam pytanie do czego dąży limx→∞(√0)? (chodzi o pierwiastek stopnia x jak na
obrazku)
Wg. Wolfram Alpha (stronka do sprawdzania funkcji itp.) ta granica w minus nieskończoności
wynosi 1, a w plus nieskończoności wynosi 0.
https://www.wolframalpha.com/input/?i=%5Clim+_%7Bx%5Cto+%5Cinfty+%7D%5Cleft(%5Csqrt%5Bx%5D%7B0%7D%5Cright)
Pierwiastek można przekształcić w potęgę co da 01/x, więc gdy x dąży do nieskończoności
obojętnie której, to potęga powinna dążyć do 0, więc 00 wynosiło by 1, natomiast jest
zupełnie inaczej. Kompletnie tego nie rozumiem i byłbym wdzięczny za wytłumaczenie problemu.
Witam, mam pytanie do czego dąży limx→∞(√0)? (chodzi o pierwiastek stopnia x jak na
obrazku)
Wg. Wolfram Alpha (stronka do sprawdzania funkcji itp.) ta granica w minus nieskończoności
wynosi 1, a w plus nieskończoności wynosi 0.
https://www.wolframalpha.com/input/?i=%5Clim+_%7Bx%5Cto+%5Cinfty+%7D%5Cleft(%5Csqrt%5Bx%5D%7B0%7D%5Cright)
Pierwiastek można przekształcić w potęgę co da 01/x, więc gdy x dąży do nieskończoności
obojętnie której, to potęga powinna dążyć do 0, więc 00 wynosiło by 1, natomiast jest
zupełnie inaczej. Kompletnie tego nie rozumiem i byłbym wdzięczny za wytłumaczenie problemu.