Obszar całki podwójnej Kjuk: Cześć, mam do policzenia całkę podwójną i nie wiem jak ugryźć jej obszar, czy byłby w stanie mi ktoś pomóc? Obszar : D = { (x,y) należy do R² , 4π² ≤ x²+y² ≤ 9π², y ≤ 0 } Z góry dziękuję za pomoc.

PW: To połowa pierścienia kołowego, w czym problem?

Kjuk: Nie wiem czy mam jakieś zaćmienie umysłu, ale nie potrafię wyznaczyć z tego granic całki

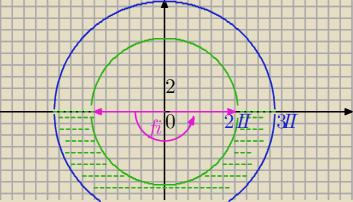
Mila: x²+y²≤(3π)², R=3π x²+y²≥(2π)², r=2π i y≤0 x=rcosφ y=r sinφ 4π≤r²cos²φ+r²sin²φ 2π≤r≤3π π≤φ≤2π P=_2π∫^3π_π∫^2πr dφ dr=_2π∫^3π[r*φ]_φ=π^2π dr= =_2π∫^3π(r*[2π−π])dr=_2π∫^3ππ*r dr=

	1
=π*[		r2]2π3π=
	2

	1		5π3
=π*		*[(3π)2−(2π)2]=
	2		2

===================

Mila: Poprawa zapisu (5 linijka) 4π²≤r²cos²φ+r²sin²φ≤9π²