Pięciokąt. Wykaż, że kąt ADB=1/2EDC Mis_tr: Pięciokąt. Wykaż, że kąt ADB=1/2EDC W pięciokącie wypukłym ABCDE spełnione są zależności CD=DE, kąt BCD=kąt AED=90° oraz BC+EA=AB. Wykaż, że kąt ADB= 1/2EDC.

Przemysław:

	1
By pokazać, że ∡ADB =		*∡EDC wystarczy pokazać, że ∡ADB=∡BDC+∡ADE
	2

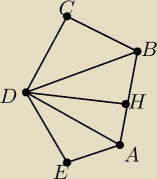
Poprowadźmy na bok BA prostą prostopadłą z wierzchołka D. Jest ona wysokością ΔABD i przecina BA w punkcie H. Pokaż, że ∡ADH=∡EDA i ∡HDB=∡BDC, a z tego wyniknie teza.