Wykaż, że z odcinków można zbudować trójkąt
Zebra: Witam, mam takie dwa zadania z geometrii z działu izometrie (obrót o kąt, symetrie, translacje)
i przystawanie trójkątów.
Punkt P należy do wnętrza trójkąta równobocznego ABC. Wykaż, że z odcinków PA, PB i PC można
zbudować trójkąt.
W pięciokącie wypukłym ABCDE spełnione są zależności CD=DE, kąt BCD=kąt AED=90° oraz BC+EA=AB.
Wykaż, że kąt ADB= 1/2EDC.
19 wrz 19:12
iteRacj@:
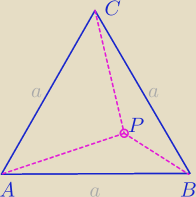
P należy do wnętrza trójkąta równobocznego ABC, więc P≠A, P≠B, P≠C
z tego wynika, że a>|PA|,a>|PB|, a>|PC|
skorzystamy z nierówności trójkąta:
|PA|+|PB|>a ⇒ |PA|+|PB|>|PC|
|PC|+|PB|>a ⇒ |PC|+|PB|>|PA|
|PC|+|PA|>a ⇒ |PC|+|PA|>|PB|
19 wrz 19:44
 P należy do wnętrza trójkąta równobocznego ABC, więc P≠A, P≠B, P≠C
z tego wynika, że a>|PA|,a>|PB|, a>|PC|
skorzystamy z nierówności trójkąta:
|PA|+|PB|>a ⇒ |PA|+|PB|>|PC|
|PC|+|PB|>a ⇒ |PC|+|PB|>|PA|
|PC|+|PA|>a ⇒ |PC|+|PA|>|PB|
P należy do wnętrza trójkąta równobocznego ABC, więc P≠A, P≠B, P≠C
z tego wynika, że a>|PA|,a>|PB|, a>|PC|
skorzystamy z nierówności trójkąta:
|PA|+|PB|>a ⇒ |PA|+|PB|>|PC|
|PC|+|PB|>a ⇒ |PC|+|PB|>|PA|
|PC|+|PA|>a ⇒ |PC|+|PA|>|PB|