Oblicz. Proszę o pomoc lub ewentualny link gdzie mogę znaleźć rozwiązanie.Dzięki filand: x³/3 − x dla x=³√√3+√2+³√√3−√2

Adamm: a=³√√3+√2, b=³√√3−√2 (a+b)³/3−(a+b) = (a³+b³)/3+(ab−1)(a+b) ab = ³√√3+√2³√√3−√2 = 1 ab−1 = 0 (a³+b³)/3 = (√3+√2+√3−√2)/3 = 2√3/3 czyli wynik to 2√3/3

PW: Może to ułatwi rachunki: (√3−√2)(√3+√2)=1, a więc

	1
(√3−√2)=		,
	(√3+√2)

czyli liczba x jest postaci

	1
3√t+
	3√t

albo inaczej

	1
u+		, u>0.
	u

PW: Przepraszam Adamm, nie widziałem.

Eta: x³=√3+√2+√3−√2+3³√√3−√2)(√3+√2)*(³√√3+√2+³√√3−√2) x³=2√3+3x x³−3x=2√3 /:3

x3
	−x=2√3/3
3

PW: Myślę że zastosowanie "u" powoduje mniej uciążliwego przepisywania tych pierwiastków

1

1

1

1

3

1

x3=(u+

)3=u3+3u2

+3u

+

=u3+3u+

+

.

u

u

u2

u3

u

u3

x3

u3

1

1

1

u3

1

−x=

+u+

+

−(u+

)=

+

3

3

u

3u3

u

3

3u3

a ponieważ u³=√3−√2,

x3		√3+√2		1		√3+√2		√3−√2		2√3
	−x=		+		=		+		=
3		3		3(√3+√2)		3		3		3

filand: Bardzo dziękuję

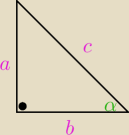
filand: W trójkącie prostokątnym naprzeciw kąta ostrego alfa leży przyprostokątna o długości a. Oblicz długość pozostałych boków trójkąta, jeśli : Przykłady : A) a = 40cm, sin alfa=0,8, B) a = 5cm, sin alfa = pierwiastek z 3/2, C) a = 3cm, cos alfa = 8/17, D) a = pierwiastek z 6 cm, cos alfa = 0,5.

chichi:

	a		4		40
sinα=		⇒		=		⇒ c=50cm (trojkat 30−40−50) ⇒ b=30cm, jak tego nie widzisz to
	c		5		c

kolejny bok można policzyć z tw. Pitagorasa. Reszta podpunktów jest twoja