 Podpowiedź:
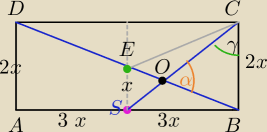
x− wspólna miara
|SE|=x jako odcinek łączący środki boków ΔBAD
Podpowiedź:
x− wspólna miara
|SE|=x jako odcinek łączący środki boków ΔBAD
| 1 | ||
ΔSOE∼ΔCOB w skali k= | ||
| 2 |
| 3x | ||
sinγ= | ||
| |SC| |
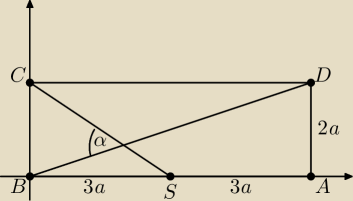 A = (6a, 0), B = (), 0), C = (0, 2a), D = (6a, 2a), S = (3a, 0)
współczynniki kierunkowe prostych
A = (6a, 0), B = (), 0), C = (0, 2a), D = (6a, 2a), S = (3a, 0)
współczynniki kierunkowe prostych
| 2a | 1 | 2a | 2 | |||||
BA: a1 = | = | oraz CS: a2 = | = − | |||||
| 6a | 3 | −3a | 3 |
| a1 − a2 | ||
tgα = | | | | |
| 1 + a1a2 |
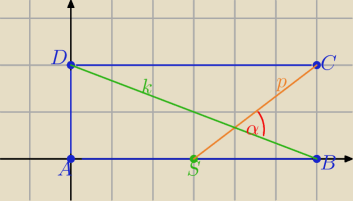 Umieszczamy prostokąt w układzie współrzędnych tak jak na rys.
A(0,0) , B(6b,0), C(6b,2b), D(0,2b) , S(3b,0)
korzystamy ze wzoru na tangens kąta między prostymi SC =p i BD=k
Umieszczamy prostokąt w układzie współrzędnych tak jak na rys.
A(0,0) , B(6b,0), C(6b,2b), D(0,2b) , S(3b,0)
korzystamy ze wzoru na tangens kąta między prostymi SC =p i BD=k
| ak−ap | ||
tgα=| | | gdzie ak , ap −− współczynniki kierunkowe prostych | |
| 1+a+k*ap |
| 2b | 2b | |||
ak= | =−1/3 i ap= | =2/3 | ||
| −6b | 3b |
| 1 | ||
to tgα=| | |=..... | |
| 1−(2/9) |
| 9 | ||
tgα= | ||
| 7 |

| ak−ap | ||
tgα= | | | | |
| 1+ak*ap |
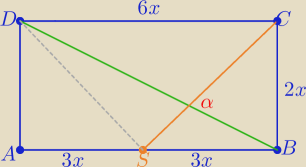 Inny sposób
Inny sposób
| 1 | ||
P(trapezuBCDS)= 9x2 i P(trapezuBCDS)= | *|SC|*|BD|*sinα | |
| 2 |
| 9 | 7 | |||
9x2=√130x2sinα ⇒ sinα= | to cosα= √1−sin2α =...= | |||
| √130 | √130 |
| sinα | 9 | |||
zatem tgα= | =...... = | |||
| cosα | 7 |