Odcinek AB o długośći 4 jest zawarty w prostej o równaniu Kiciaw: y= 34x − 32. Symetralna odcinka AB przecina oś OY w punkcie (0,6). Oblicz współrzędne końców odcinka AB. Chciałam to zrobić z układu równań i wzoru na współrzędne punktu po środku. Czyli (X1+x2)/2=18/5 i (3/4 x1−3/2+3/4x2−3/2)/2= 6/5. Wychodzi mi układ nieoznaczony. Dlaczego?

Mila: Równanie prostej to

	3		3
y=		x−		?
	4		2

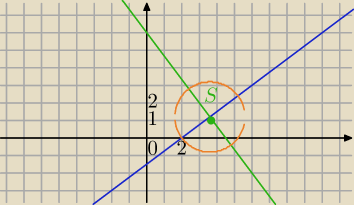
Mila: Nie uwzględniłaś długości odcinka, jest nieskończenie wiele odcinków o środku w punkcie przeciecia prostej AB i symetralnej

	3		3
k: y=		x−
	4		2

1) Symetralna AB

	4
y=−		x+6
	3

2) Punkt przecięcia prostych to środek AB

	4		3		3
−		x+6=		x−
	3		4		2

	18		6
S=(		,		)
	5		5

3) równanie okręgu o środku S i r=2 (x−U{18})²+(y−U{6}{5)²=2² 4) punkty przecięcia okręgu z prostą k

	18		3		3		6
(x−		)2+(		x−		−		)2=4
	5		4		2		5

(x−18/5)²+(3/4x−27/10)²=4 x=2 i y=0 lub

	26		12
x=		i y=
	5		5

	26		12
A=(2,0), B=(		,		)
	5		5

sprawdź rachunki.

Eta: https://matematykaszkolna.pl/strona/4124.html

Kiciaw: Mila, dziękuję, o to mi chodziło. Nie pomyślałam o tym, że jest nieskończenie wiele punktów, które dadzą taki wynik. Zrobiłam w końcu uwzględniając długość, ale nadal próbowałam też zrobić to z układu równań.