pole trójkąta Kamil: Oblicz pole trójkąta ostrokątnego ABC w którym : bok AB=5, wysokość BD=4 i środkowa AE=4,5 Zadanie na poziomie gimnazjum

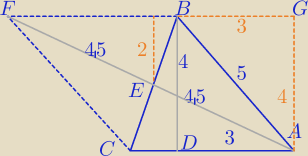
iteRacj@: |AB|=5, |BD|=4 |AE|=4,5 |CE|=|EB| |FB| || |CA| , |FC| || |BA| |FA|=2*|AE|=2*4,5=9 |GA|= |BD|=4 z tw.Pitagorasa dla ΔFGA: |FG| = √9²−4²=2√5

	1
PΔFGA=		*2√5*4=4√5
	2

|BG|=|AD|=3

	1
PΔBGA=		*3*4=6
	2

P_ΔABC=P_ΔFBA=P_ΔFGA−P_ΔBGA=4√5−6 rozwiązanie na poziomie gimnazjum

Eta: Wkradł się chochlik: |FG|=√81−16=√65

iteRacj@: dzięki, w nowym roku szkolnym popracuję nad precyzją obliczeń

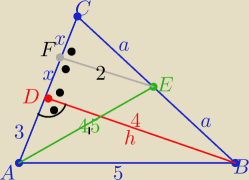Eta: Inny sposób: 1/ z tw. Pitagorasa w ΔABD : |AD|=3 2/ EF|| BD i z tw. Talesa |EF|=2 i |DC|=2x , x>0 i |DF|=|FC|=x 3/ z tw. Pitagorasa w ΔAEF : (x+3)²+2²=4,5²

	65		√65
to (x+3)2=		⇒ x+3=		⇒ 2x=√65−6
	4		2

P(ABC)= (2x+3)*h/2 P(ABC)=2(√65−3) ================