Domknięcia Psikuta: Hejka, mam problem z jeszcze jednym zadaniem − chodzi o relacje binarne i domknięcia Wyznacz domknięcia: p(R), z(R), s(R), s(p(R)), z(s(R)) i klasy abstrakcji p(s(z(R))) // z − zwrotne, s − symetryczne, p − przechodnie gdzie R ⊆ {1,2,3}² ⋀ R = {(1,2), (3,3)} p(R) = R z(R) = R ∪ {(1,1), (2,2)} s(R) = R ∪ {(2,1)} s(p(R)) = R ∪ {(2,1)} p(s(R)) = R ∪ {(2,1), (1,1), (2,2)} Tylko nie wiem o co chodzi z tymi klasami abstrakcji p(s(z(R))) Być może jakieś dziwne oznaczenia stosuję albo w ogóle dziwne zadanie ale takie u nas na wykładach było więc chyba nie jest źle

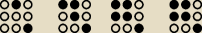
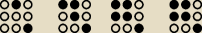Pytający: Od lewej kolejno "tabelki" relacji: R, z(R), s(z(R)), p(s(z(R))). Stąd widać, że dla Q=p(s(z(R))) są dwie klasy abstrakcji: [1]_Q=[2]_Q={1,2} [3]_Q={3}