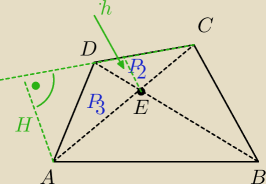
nierówność geometryczna piotmni: W czworokącie wypukłym ABCD przekątne AC i BD przecinaja się w punkcie E. Trójkąty ABE i CDE mają pola odpowiednio P₁ I P₂ , a czworokąt ABCD ma pole P. Wykaż, że: √ P₁ + √P₂ <= √P przyjmujemy jeszcze że AED to P₃, a BEC to P₄. nie chodzi mi o samo rozwiązanie, ponieważ mam dostępne rozwiązanie, chociaż jeśli ma ktoś oryginalny pomysł to proszę, ale w jednym sposobie rozwiązania jest przyjęte, że P₃= P₂*AE/EC i P₄ = P₁ * EC/AE czy mógłby ktoś wytłumaczyć dlaczego ?

Blee: z tw. Talesa:

h		CE
	=
H		AC

	P2		CE		P2+P3		AE + CE		P3
więc		=		⇔		=		⇔		=
	P2+P3		AE + CE		P2		CE		P2

	AE
	CE

analogicznie druga równość

iteRacj@:

	1
P3=		h1*|AE|
	2

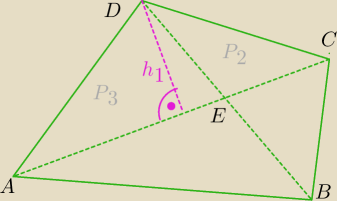
	1		1		P2
P2=		h1*|CE| ⇒		h1=
	2		2		EC

	P2*|AE|
P3=
	|EC|

piotmni: dzięki bardzo