Zbiory - element maksymalny/największy aram: Hej Czy mógłby ktoś jak debilowi wytłumaczyć różnicę między elementem maksymalnym i największym w jakimś zbiorze? (minimalny i najmniejszy to pewnie analogicznie) Przeczytałem parę postów w Internecie i nic nie rozumiem, a z definicji podanej na wykładzie to dla mnie jest to samo... Jakiś prosty przykład może być Z góry dziękuję

PW: "Maksymalny" i "największy" to synonimy. Pewnie rozważasz, czy taki element w zbiorze istnieje, czy nie − ale to już inna sprawa.

ite: a może (takie zgadywanie) chodzi o element maksymalny i największy nie − tak jak napisano − w jakimś zbiorze, ale w zbiorze częściowo uporządkowanym ?

aram: Kurna, właśnie o to mi chodziło, przepraszam że nie sprecyzowałem

vev: To jest to samo

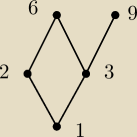
Pytający: To nie to samo. Łopatologicznie (pisałeś, że definicję masz) w zbiorze częściowo uporządkowanym: • element minimalny (maksymalny) to taki element, że w ów zbiorze nie ma elementów od niego mniejszych (większych); może być kilka takich elementów, • element najmniejszy (największy) to taki element, który jest mniejszy (większy) od wszystkich pozostałych elementów tegoż zbioru; jeśli istnieje, jest to jedyny element minimalny (maksymalny) tego zbioru. Przykładowo (pomocniczo patrz rysunek (diagram Hassego)): • w zbiorze {1,2,3,6,9} uporządkowanym relacją podzielności: − element najmniejszy: 1 − element największy: brak − elementy minimalne: 1 − elementy maksymalne: 6, 9 • w zbiorze {1,2,3,6} uporządkowanym relacją podzielności: − element najmniejszy: 1 − element największy: 6 − elementy minimalne: 1 − elementy maksymalne: 6 • w zbiorze {2,3,6,9} uporządkowanym relacją podzielności: − element najmniejszy: brak − element największy: brak − elementy minimalne: 2, 3 − elementy maksymalne: 6, 9 • w zbiorze {2,3,6} uporządkowanym relacją podzielności: − element najmniejszy: brak − element największy: 6 − elementy minimalne: 2, 3 − elementy maksymalne: 6

aram: Dziękuję Ci Bardzo Pytający, teraz już wszystko rozumiem