Proszę O Pilną Pomoc ( Sprawdzian na pierwszej lekcji matematyki) - Parametry M2001: Zaraz po wakacjach czeka mnie sprawdzian z matematyki. Niestety mam problem z kilkoma zadaniami. Zadanie 1) Wyznacz wszystkie wartości parametru k, dla których wykres funkcji f(x) = −2x² +4x +k ma trzy punkty wspólne z osiami układu współrzędnych. Ma Wyjść: k∊(−2;0) ∪ (0 ; ∞ ) Zadanie 2) Dla jakich wartości parametru p zbiorem wartości funkcji f(x) =(1−p²)x² − 2(p−1)x −2 jest zbiór liczb niedodatnich? Rozwiązaniem powinno być : dla p = −3 Zadanie 3) Dla jakich wartości parametru m dziedziną funkcji f(x) = {x² +(m+1)x −m + 2} jest zbiór liczb rzeczywistych? Rozwiązanie powinno wyjść : dla m∊<−7;1> Zadanie 4) Wyznacz wszystkie wartości parametru m, dla których iloczyn pierwiastków równania x² − (m+1)x + m² −5 =0 Rozwiązaniem powinno być: dla m = {6} Zadanie 5) Dla jakich wartości parametru k suma kwadratów pierwiastków równania x² − (k +1)x −3 −k =0 jest najmniejsza ? Rozwiązaniem powinno być: k=−2 Zadanie 6) Wyznacz wszystkie wartości parametru a, dla których równanie x² − 2ax − a +2 ma dwa różne rozwiązania mniejsze od −1 Rozwiązaniem powinno być: a∊(−3;−2) Zadanie 7) Wiadomo, że funkcja f(x) = (p² −1)x² − {2}p(p−1)x − 17π osiąga wartość najmniejszą. Wówczas p< −1 lub p≥1 Tu Proszę O Wytłumaczenie Dlaczego Zadanie 8) Wyznacz wartość najmniejszą I wartość największą funkcji f(x) = 3 / 2x −5x +5 w przedziale <1;2> Rozwiązaniem powinno być: najmniejsza;1 , największa 8/5 Przepreszam za wielką ilość zadań ale mam nadzieję że ktoś zdoła szybko mi pomóc. Niestety moja nauczycielka poświęciła parametrom zaledwie dwie godziny lekcyjne nie przytaczając nawet powyższych przykładów które jednak pojawią się na sprawdzianie.

Jerzy: Zad 1) Skoro ma jeden punkt wspólny z osią OY ( tak jest zawsze ), to musi mieć dwa wspólne z osią OX, czyli musi mieć dwa miejsca zerowe, czyli musi być spełniny warunek ...... ?

Jerzy: Zad 2) Skoro zbiór liczb niedodatnich, to gałęzie skierowane w dół i wykres styczny do osi OX, czyli jedno miejsce vzerowe. Zatem muszą być spełnine 2 waruki: współczynnik przy x² ujemny i Δ = 0

Jerzy: Zad 3) Co oznaczaja te klamry po obu stronach trójmianu ?

Jerzy: Zad 4) Dokończ treść zadania.

Jerzy: Zad 5) Przypomnij sobie ( poszukaj ) wzory Viete'a i wskazówka: x₁² + x² = ( x₁ + x₂)² − 2 x₁*x₂)

Jerzy: Zad 6) Warunki: 1) Δ > 0 2) x_w < −1 ( x_w − odcieta wierzchołka) 3) f(−1) > 0

Jerzy: Teraz działaj sam, a my Ci pomozemy.

M2001: 1) Czyli Δ>0 ? 3) Oznaczają Pierwiastek Nad całym równaniem. Przepraszam Jestem tutaj nowa na forum i źle to zapisałam 4) Tak Nie dokończylam Jest równy 1

Jerzy: Zad 1) Tak , to jedyny warunek ....działaj i pokaż jak liczysz.

M2001: Niestety Mam problem ze srawianiem warunków. Zad. 6 Rozumiem dwa pierwsze warunki tylko nie wiem co zrobić z trzecim czyli f(−1) >0 Chodzi O To By jako x postawić −1 ?

Jerzy: Zad 3) Trójmian musi przyjmować tylko wartości nieujemne, czyli: 1) gałezie do góry ( jaki warunek ?) 2) jedno miejsce zerowe ( jaki warunek ?)

Jerzy: Zad 6) Policzyć wartośc funkcji (trójmianu) dla argumentu x = 1 ( podstawic za x liczbe −1)

Jerzy: Pokaż obliczeniea dla zadania 1)

M2001: Dobrze 1. Δ> 0 Δ = 16 − 4 × (−2k) = 16 + 8k 16 + 8k > 0 8k > −16 k> −2 k∊(−2; ∞) Ale To Nie Pełna Odpowiedź

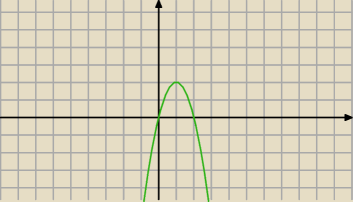
Jerzy: Tak, to moje niedopatrzenie. Popatrz na wykres dla k = 0 , wykres przechodzi przez początek układu, czyli wykres ma tylko 2 punkty wspólne.

Jerzy: Czyli musimy dołożyć drugi warunek: f(0) ≠ 0 ⇔ k ≠ 0

M2001: 2) Δ = 0 Δ = (−2(p−1))² − 4× (1−p²) × (−2) = 4p² +4p +8 =0 I Co Dalej ?

M2001: A No Tak Teraz Rozumiem

M2001: Czy W Tym Drugim Teraz Obliczem Δp?

M2001: 3) Ramiona Skierowane Ku Górze Czyli wspolcznik przy x² jest dodatni Jedno Miejsce Zerowe Więc Δ= 0

M2001: Ale Co Zrobić W Tym 3 Z Tym Pierwiastkiem Na Górze?

the foxi: zadanie 7: Wiadomo, że funkcja f(x) osiąga wartość najmniejszą. czyli parabola jest "uśmiechnięta", zatem współczynnik przy x² musi być dodatni p²−1>0 (p−1)(p+1)>0 p<−1 lub p>1

M2001: Okej Czyli 1 i 7 Już Rozumiem Dziękuję

Jerzy: Zad 3). Jedyny warunek: Δ = 0 , bo gałęzie są do góry ( dlaczego ? )

Jerzy: Drobna korekta: Δ ≤ 0

M2001: Mam Pytanie Co Do Zadania 4 Tam Ma Być Pierwiastek Z 6 Ale Według Moich Obliczeń Wychodzi Zarówno Pierwiastek Z 6 Jak I Z Minus 6 I Nie Wiem Dlaczego W Rozwiązaniu Nie Ma Podane Również Pierwiastka Z Minus 6 Moje Obliczenia: c/a=1 m² −5 = 1 m² = 6 m= √6 lub m = √−6 ?

M2001: Cofam Pytanie Nie Uwzględnilam Zakresu M

M2001: Mam Już Zadanie 1,4,7

PW: Zadanie 4) Wyznacz wszystkie wartości parametru m, dla których iloczyn pierwiastków równania x² − (m+1)x + m² −5 =0. − Taką podałeś treść. Co iloczyn pierwiastków?

PW: A, gdzieś dokończyłeś: jest równy 1.

M2001: Mam Już Też 5 Prosiła Bym O Pomoc Z 2,3,6,8

M2001: Miało Być Na Końcu: Jest Równy 1

M2001: Ale Udało Mi Się Już To Zrobić

Jerzy: Zad 2) Patrz wczoraj 12:29

M2001: Liczę To 2 Ale Nie Potrafi Mi To Wyjść Czy Ja Dobrze Liczę Tą Δ? Δ = (−2(p−1))² − 4× (1−p²)(−2) Δ= (−2p +2) ² − 4× (−2+ 2p⁾ Δ= 4p² −8p + 4 + 8 + 8p Δ = 4p² + 12 4p² + 12 = 0 4p² = −12 p² = −3 Coś Tu Nie Pasuje Bo Rozwiązanie Ma Być p= −3

Jerzy: Źle trzecia linijka.

M2001: Czy To ( −2p + 2)² Zapisywać Jaki Zwhkldy Wzór Skróconego Mnożenia

M2001: *Zwykły

Jerzy: Δ = 4p² − 8p + 4 + 8 − 8p

M2001: Dziękuję Bardzo

M2001: Czy Teraz Mam Liczyć Δp?

Jerzy: Tak i wyjdzie Ci ,że Δ = 0 dla p = 1 lub p = 3 Z pierwszego warunku mamy: 1 − p² < 0 ⇔ p < −1 lub p > 1, a więc ostatecznie rozwiazaniem zadania jest : p = 3 ( a nie p = −3). Sprawdź jeszcze raz treść zadania.

M2001: Niestety Po Ponownym Sprawdzeniu Treść Zadania Się Zgadza A W Odpowiedziach Jest Minus 3 Ale To Zadania Z Nowej Ery Więc Może Jest To Błąd

M2001: Mogę Prosić Teraz O Pomoc Z 3? Napisze Go Jeszcze Raz

M2001: Dla jakich wartości parametru m dziedziną funkcji f(x) = √x2 +(m+1)x −m + 2 jest zbiór liczb rzeczywistych? Rozwiązanie powinno wyjść : dla m∊<−7;1>

M2001: Od Czego Zacząć Co Zrobić Z Pierwiastkiem ?

Jerzy: Teraz widze, gdzie popeniłaś błąd: Δ = [−2(p − 1)]² − 4(1 − p²)(−2) = 4(p² − 2p + 1) + 8 − 8p² = 4p² − 8p + 4 + 8 − 8p² = −4p² − 8p + 12

Jerzy: Najpierw popraw zad 2) , a potem zrobisz 3

Jerzy: Zad 3) Warunek: x² + (m + 1)x − m + 2 ≥ 0 Gałęzie są skierowane do góry ( dlaczego ?) , wiec wystarczy aby: Δ ≤ 0

M2001: Już Poprawiam

M2001: W 3 Gałęzie Do Góry Bo Współczynnik Dodatni Przy x²

M2001: 3 Udało Mi Się

Jerzy: Tak. Dokończ 2 , rzeczywiście rozwiązaniem jest: p = −3

M2001: Zostało Mi Jeszcze 6 I 8

M2001: 6 Nie Rozumiem Kompletnie Nie Wiem Jak Stawia Się Te Warunki

M2001: 2 Poprawilam I Wyszło

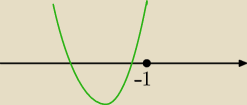
Jerzy: Popatrz na rysunek. Ta parabola spełnia awarunki zadania, a więc: 1) Δ > 0 ( bo muszą być dwa pierwiastki) 2) x_w < −1 ( x_w − odcięta wierzchołka , patrz na rysunek ) 2) f(−1) > 0 ( patrz na rysunek , celowo odsunąłem punkt x = −1 za bardzo w prawo)

M2001: Dziękuję Spróbuję Teraz Rozwiązać

M2001: Wyszło Mi 6 Dziękuję Zostaje Jeszcze 8

Jerzy: Zapisz poprawnie treść.

M2001:

	3
Wyznacz wartość najmniejszą I wartość największą funkcji f(x) =		w
	2x2 −5x +5

przedziale <1;2> Rozwiązaniem powinno być: najmniejsza;1 , największa 8/5

Jerzy: Najpierw musimy ustalić dziedzinę funkcji f(x), czyli warunek: 2x² − 5x + 5 ≠ 0 W drugim kroku musimy poszukać najmniejszą i najwiekszą wartość funkcji: g(x) = 2x² − 5x + 5 w podanym w treści zadania przedziale...... działaj.

M2001: Jak Ustalić Tą Dziedzinę? Bo Delta Wychodzi Mi Na Minusie

Jerzy: No i dobrze,bo jest ujemna, więc jakie wnioski ?

Jerzy: Krótko mówiąc, czy funkcja g(x) = 2x² − 5x + 5 przyjmuje wartość 0 ?

M2001: Nie Przyjmuje ?

Jerzy: Oczywiście nie przyjmuje. Czyli mianownik funkcji f(x) nigdy się nie zeruje, a więc dziedziną funkcji f(x) jest: D = R Teraz drugi krok.

M2001: Czyli Poprostu Podstawiać Jako x 1 I 2?

piotr:

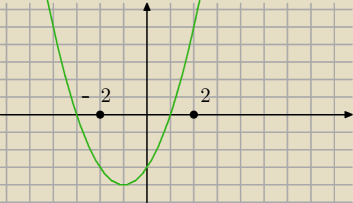
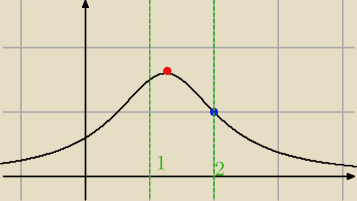
Jerzy: NIe do końca...popatrz na rysunek , jaka jest najmniejsza i najwieksza wartośc tej funkcji w przedziale <−2;2> ?

Jerzy: @piotr .. wciąłeś się, podając "gotowca", a nie o to chodzi. Ja chcę pomóc jej zrozumieć rozwiazanie tego zadania,

M2001: Najmniejsza To −4 A Największa 5

Jerzy: A widzisz ! Czyli najpierw musimy sprawdzić, czy odcięta wierzchołka paraboli g(x) = 2x² − 5x + 5 należy do przedziału <1;2> bo wtedy dla tego x funkcja g(x) będzie miała minimum. Licz: g(1) g(2) g(x_w) potem wybierz najmniejszą i największą wartość.

Jerzy: popwinienem był napisać: ....będzie miała najmniejszą wartość w przedziale <1;2>

M2001:

	3
g(1) =
	2

g(2) = 1

M2001:

	5
xw To		?
	4

Jerzy: Skup się ! Liczymy wartości funkcji g(x) , czyli mianownika g(x) = 2x² − 5x + 5

Jerzy:

	5
Tak. xw =
	4

M2001:

	8
Wtedy Wyjdzie
	5

I Najmniejsza Będzie Dla g(1) Największa Dla g(Xw) ?

M2001: Dziękuję Wszystkim Za Pomoc @Jerzy Wiele Zrozumiałam

Jerzy: Na pewno zrozumiałaś rozwiązanie zadania 8 ?

M2001: Tak Jeśli Xw Należy Do Zakresu Podanego W Zadaniu To Tam Będzie Największa Wartość Funkcji

Jerzy: Funkcja f(x) osiąga maksimum, gdy mianownik g(x) = 2x² − 5x +5 osiąga minimum i odwrotnie.

	5
Funkcja g(x) ( mianownik ) osiąga minimum dla x =		, a maksimum dla x = 2
	4

piotr: f_max(q)=f(5/4)=8/5

M2001: Dziękuję

M2001: Podsumowując : fmin= f(2) =1 fmax= f(5/4)= 8/5

M2001: W Końcu Wszystko Rozwiązane

Jerzy: Czemu każdy wyraz piszesz dużą literą ?

M2001: Piszę z telefonu i choć napisze z malej przeskakuje mi i nie chce mi się tego zawsze pilnować