wykaż Dawid: Witam Nie mogę sobie poradzić z takim oto zadaniem o treści: Dany jest okrąg o środku S , z punktu P leżącym poza tym okręgiem poprowadzono dwie styczne PA i PB ( A i B punkty styczności) Prosta AB przecina prostą PS w punkcie M Z punktu P poprowadzono prostą k (nie zawierającą średnicy)która przecina ten okrąg w punktach C i D Wykaż że punkty S,M,C,D leżą na jednym okręgu Pomoże mi ktoś ? bardzo proszę

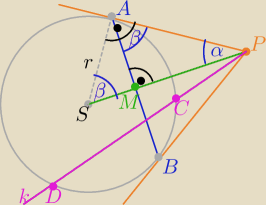
Eta: 1/ jak zwykle w geometrii : przejrzysty rysunek zgodny z treścią zadania 2/korzystamy z twierdzenia o stycznej AP i siecznej PD |AP|²=|PC|*|PD| 3 / z podobieństwa trójkątów APS i APM z cechy (kkk)

	|AP|		|MP|
		=		⇒ |AP|2=|SP|*|MP|
	|SP|		|AP|

zatem z 2/ i 3/ mamy : |PC|*|PD|=|MP|*|SP| a to jest równość między siecznymi w okręgu do którego należą punkty : S,M,C,D co kończy dowód

Eta: Może Mila poda jeszcze inny sposób

Mila: Nic dodać nic ująć Może tylko zacytować twierdzenie, jeśli autor nie zna.

ElizaR: Jest jeszcze inny sposób; niemal automatyczny: za pomocą liczb zespolonych na okręgu jednostkowym Szkic dowodu: Mamy A(a), B(b), S(0), P(2ab/(a+b)),M((a+b)/2), oraz przyjmujemy C(c). A wtedy d = (ac+bc−2ab)/(2c−a−b) ( otrzymane z warunku przynależności punktu P do prostej (CD): _ p = (c+d −p)/cd ) Sprawdzamy, że dwustosunek czwórki punktów [ 0, a+b/2, c, (ac+bc−2ab)/(2c−a−b) ] jest liczbą rzeczywistą... W komuniźmie na matematyce w liceum uczono liczb zespolonych. Teraz w zamian uczą religii...

gg: @ElizaR "W komuniźmie na matematyce w liceum uczono liczb zespolonych. Teraz w zamian uczą religii..." Religii uczą ale przecież nie na matematyce.

ElizaR: @ gg: to skrót myślowy: matematyka i nauki przyrodnicze zostały świadomie okrojone bo to, by stworzyć przestrzeń czasową do nauczania religii. Czas spędzony w szkole wszak nie jest z gumy... W szkole po 1989 roku priorytetem kształcenia stała się nauka rytuałów i zabobonów religijnych, w tym celu np. świadomie usunięto logikę z licealnych programów nauczania, ostatnio nawet wnioskowanie indukcyjne...Ot, « dobra zmiana » w reformie programów szkolnych: Polska jest jedynym krajem w Europie, gdzie na poziomie szkoły średniej nie uczy się indukcji zupełnej. A Zofia Krygowska się w grobie przewraca...