pola
szymek:
W trapez równoramienny o polu 5 wpisano okrąg o promieniu 1
Wyznacz stosunek pola czworokąta którego wierzchołkami są punkty styczności okręgu
z trapezem do pola trapezu
18 sie 23:08
Mila:
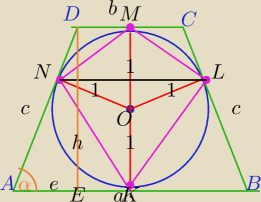
1)
a+b=5
2c=a+b
c=2.5
2)
3) W ΔAED:
e
2+h
2=c
2⇔2.5
2=e
2+2
2
e
2=2.25⇔e=1.5
e=(a−b):2⇔1.5=(a−b):2
a−b=3
a+b=5 stąd a=4 i b=1
Pola naroży:
| | 1 | | a | | a | | b | | b | |
Pn=2* |
| * |
| * |
| *sinα+2* |
| * |
| *sin(180−α)= |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
| | 1 | | 4 | | 1 | | 1 | | 1 | | 4 | |
=2* |
| *2*2* |
| +2* |
| * |
| * |
| * |
| = |
| | 2 | | 5 | | 2 | | 2 | | 2 | | 5 | |
====================
3)
===========================
19 sie 00:12
Mila:
Jest Eta !, może poda inny sposób z podobieństwa.
19 sie 00:13
Eta:
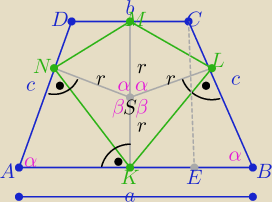 Jeden ze sposobów
Jeden ze sposobów
Z treści zadania : P=5 ⇒ a+b=5
z warunku wpisania okręgu w trapez : 2c=a+b ⇒ c=5/2
W ΔEBC: sinα= 4/5
α+β=180
o to sinα=sinβ
| | 1 | |
P(KLMN)= 4* |
| r*r*sinα ⇒P=8/5 |
| | 2 | |
===========
19 sie 00:19
Eta:

19 sie 00:23
Mila:
Pięknie!

Dobranoc

19 sie 00:28
Eta:
Dobranoc

19 sie 00:31
Eta:
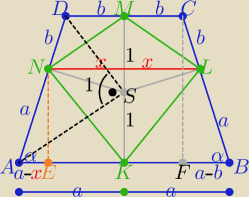
Jeszcze taki sposób

Z treści zadania : a+b=5/2 i w ΔASD : ab=r
2
a+b=5/2 i ab=1 ⇒ a= 2 i b=1/2 bo a>b
z podobieństwa trójkątów AED i FBC
| a−x | | a−b | |
| = |
| ⇒ ... x=4/5 |
| a | | a+b | |
to
P=8/5
============
19 sie 00:45
szymek:
Super wielkie dzięki!
19 sie 15:23
Mila:

19 sie 16:02
 1)
1)
 Jeden ze sposobów
Z treści zadania : P=5 ⇒ a+b=5
z warunku wpisania okręgu w trapez : 2c=a+b ⇒ c=5/2
W ΔEBC: sinα= 4/5
α+β=180o to sinα=sinβ
Jeden ze sposobów
Z treści zadania : P=5 ⇒ a+b=5
z warunku wpisania okręgu w trapez : 2c=a+b ⇒ c=5/2
W ΔEBC: sinα= 4/5
α+β=180o to sinα=sinβ

 Dobranoc
Dobranoc

 Jeszcze taki sposób
Jeszcze taki sposób 
