1.163 4 nierówności logaryt manna: 1.163 rozwiąż 4 nierówności a) log_1/3 x>log_x 3 − 2.5 b)log₂ (x−1) − log₂ (x+1) + log_{(x+1)/(x−1)} 2 >0 c)log_x/2 8 + log_x/4<(log₂ x⁴)/(log₂ x²−4) d) log_x 2 *log_2x 2 * log ₂ 4x>1 Jakoś nie potrafię zrobić ani jednego przykładu dobrze. Ktoś podoła temu zadaniu? Będę wdzięczny za każdy przykład.

manna: Jeszcze dodam odpowiedzi: a) (0,1)u(√3,9) b) (3,+∞) c) (0,2)u(4,+∞) d) (2^−√2,1/2)u(1,2^√2)

the foxi:

	log1/33
a) logx3=
	log1/3x

	log22
b)log(x+1)(x−1)2=
	log2[(x+1)(x−1)]

	log28
c)logx/28=
	log2(x/2)

	log22
d)logx2=
	log2x

	log22
log2x2=
	log22x

wzory na zamianę podstaw logarytmu, na pewno pomogą!

manna: znam ale gdzieś robie błędy przy przekształcaniu a takie ciężko znaleźć dlatego prosze o pomoc jak za dużo roboty to ok, trudno

the foxi: a zrobię sobie a) (x>0 ∧ x≠1 ∧ x>0) ⇔ x∊(0;+∞)\{1} log_1/3x>log_x3−2.5

	log1/33
log1/3x>		−2.5
	log1/3x

	1
log1/3x>−		−2.5
	log1/3x

t=log_1/3x

	1
t>−		−2.5
	t

t2		1		2.5t
	+		+		>0
t		t		t

t2+2.5t+1
	>0
t

t(t²+2.5t+1)>0 t(t+0.5)(t+2)>0 t∊(−2;−0.5)∪(0;+∞) czyli mamy trzy nierówności do rozwiązania t>0 ∨ (t>−2 ∧ t<−0.5) log_1/3x>0 ∨ (log_1/3x>−2 ∧ log_1/3x<−0.5) log_1/3x>log_1/3(1/3)⁰ ∨ (log_1/3x>log_1/3(1/3)⁻² ∧ log_1/3x<log_1/3(1/3)^−0.5) x<1 ∨ (x>9 ∧ x>√3) biorąc te rozwiązania i uwzględniając dziedzinę, dostajemy x∊(0;1)∪(√3;9)

Mila: a) x>0 i x≠1

log3x		log33		5
	>		−		⇔
log3(1/3)		log3x		2

	1		5
−log3x>		−
	log3x		2

	1		5
−log3x−		>−
	log3x		2

	1		5
log3x+		<
	log3x		2

log₃x=t

	1		5
t+		<
	t		2

1) t>0⇔x>1

	5
t2−		t+1<0
	2

	9
Δ=
	4

	2.5−1.5		2.5+1.5
t=		lub t=
	2		2

	1
t=		lub t=2
	2

	1
t∊(		,2)
	2

1
	<log3x<2 i x>1
2

log₃(√3)<log₃x<log₃(3²} √3<x<9 lub 2) t<0⇔x∊(0,1)

	1		5
t+		<		/*t
	t		2

	5
t2−		t+1>0
	2

√Δ=1.5

	1
t=		lub t=2
	2

	1
t<		lub t>2
	2

	1
log3x<		lub log3x>2
	2

[log₃x<log₃(√3) lub log₃x>log₃9 ] i x∊(0,1) [x<√3 lub x>9 ] i x∊(0,1)⇔ x∊(0,1) odp. x∊(0,1) lub √3<x<9 ======================

Mila: Witaj foxi, napisz który przykład robisz, abyśmy nie dublowali wpisów.

the foxi: Hej, mam chwilkę czasu, to wezmę c)

Mila: Rozwiązuję (b)

manna: Po podstawieniu za t pozbyłem sie t w ułamku i tym samym nie miałem 0 na rysunku i mi się znaki odwróciły. Ty chyba też masz na końcu zły znak: x>9 a powinno być x<9. Dzięki wielkie!

the foxi: manna, przykład c) nie jest przepisany w całości (brak liczby logarytmowanej w drugim składniku po lewej stronie nierówności)

manna: fakt tam powinno być 8 czyli log_x/4 8

Mila: b)log₂ (x−1) − log₂ (x+1) + log_{(x+1)/(x−1)} 2 >0 D:

	x+1
x>1 i x>−1 i		>0⇔x>1
	x−1

	(x−1)		log2(2)
log2		+		>0⇔
	x+1		x+1   log2   x−1

	(x−1)		−1
log2		+		>0
	x+1		x−1   log2   x+1

	(x−1)		1
log2		−		>0
	x+1		x−1   log2   x+1

	(x−1)
log2		=t
	x+1

	1
t−		>0 /*t2
	t

t³−t²>0 t*(t²−1)>0 t*(t+1)*(t−1)>0 −1<t<0 lub t>1

	x−1		x−1
−1<log2		<0 lub log2		>1 i x>1
	x+1		x+1

	1		x−1		x−1
log2(		)<log2		<log2(1) lub log2		>log2(2)
	2		x+1		x+1

1		x−1		x−1
	<		<1 lub		>2 /*(x+1) (ponieważ x+1>0 dla x∊D)
2		x+1		x+1

1		1
	x+		<x−1<x+1 lub x−1>2x+2
2		2

x>3 lub x<−3 i x>1 x>3 ============

manna: Dziękuje Mila

the foxi: nie wiem, z której strony ugryźć c), żeby wynik wyszedł taki jak w odpowiedziach. może ktoś inny zrobi

Mila: d) log_x 2 *log_2x 2 * log 2( 4x)>1

	1
x>0 i x≠1 i x≠
	2

1
	*U{1}{log2(2x)*log 2( 4x)>1⇔
log2x

	1
U{1}{log2(x)*		*[ log2(4)+log2(x)]>1
	log2(2)+log2(x)

log₂(x)=t i x∊D

2+t
	>1
t*(t+1)

2+t−t2−t
	>0
t*(t+1)

2−t2
	>0⇔
t*(t+1)

(√2−t)*(√2+t)*t*(t+1)>0 t∊(−√2,−1) lub (0,√2)⇔ −√2<log₂x<−1 lub 0<log₂x<√2 log₂(2^−√2<log₂x<log₂(2⁻¹ ) lub log₂(1)<log₂x<log₂(2^√2)⇔

	1
x∊(2−√2,		)∪(1,2√2)
	2

==========================

Mila: c) Mann napisz dziedzinę, resztę liczę.

Eta:

	3		3		2log2x
c)		+		<		i x>0
	log2x −1		log2x−2		log2x−2

log₂x=t

3		3		2t
	+		−		<0
t−1		t−2		t−2

.................. (t−2)(t−1)(−2t²+4t−9)<0 ( t−2)(t−1)>0 t<1 v t>2 log₂x<1 lub log₂x>2 i x>0 odp: x∊(0,2) U (4,∞) =================

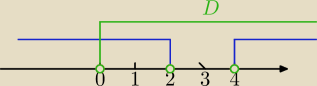
Mila: D: x>0 i x≠2 i x≠4 log_x/2 (8) + log_x/4(8)<(log₂ (x⁴))/(log₂ x²−4) dla x>0

3		3		4log2(x)
	+		<		⇔
log2(x/2)		log2(x/4)		2log2x−4

3		3		2log2(x)
	+		<
log2(x)−log2(2)		log2(x)−log2(4)		log2x−2

log₂x=t

3		3		2t
	+		<		⇔
t−1		t−2		t−2

3		3		2t
	+		−		<0
t−1		t−2		t−2

3		3−2t
	+		<0
t−1		t−2

3*(t−2)		(3−2t)*(t−1)
	+		<0
(t−1)*(t−2		(t−1)*(t−2)

3t−6+3t−3−2t2+2t
	<0⇔
(t−1)*(t−2)

U{−2t²+8t+9}{(t−1)*(t−2)<0 [n[Licznik ujemny dla każdego t∊R (Δ<0), to mianownik musi byc dodatni]] (t−1)*(t−2)>0 ⇔ t<1 lub t>2 log₂x<1 lub log₂x>2 i x∊D [x<2 lub x>4 ] i x>0 i x≠2 i x≠4⇔ x∊(0,2)∪(4,∞) ================

manna: Dziękuje wszystkim za nieocenioną pomoc