obwód trójkąta i okręgi ElizaR: Przyjmując tradycyjne oznaczenia dla trójkąta: p − połowa obwodu; r − promień okręgu wpisanego; R − promień okręgu opisanego, wykazać, że r + R > ¹₂p .

ElizaR: Mały komentarz: znana jest ( od 1966 roku ) mocniejsza NIERÓWNOŚĆ BLUNDONA: p ≤ ( 3√3 − 4)r + 2R z której wynika natychmiast nasza, słabsza... Czy można tę naszą, słabszą udowodnić prościej niż nierówność Blundona? ( najprostszy dowód nier. Blundona jest tutaj: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=2ahUKEwjG8qrH7O7cAhXhZpoKHWP4ANwQFjAAegQIABAC&url=https%3A%2F%2Fwww.emis.de%2Fjournals%2FJIPAM%2Fimages%2F220_08_JIPAM%2F220_08.pdf&usg=AOvVaw3mi54Zmxeel7-GFMGIFSm_ Dziękuję z góry za sugestie!

ElizaR: Nikt nie podejmuje wyzwania... Gdzie się podziali prawdziwi matematycy na tym forum? Są jeszcze na wakacjach?

aga: Na tym forum nie ma prawdziwych matematyków... Jedynie spoko jest jeszcze Adamm, ale on też zawsze za mało rozpisuje albo w ogóle niezrozumiale... Więc też jest nienajlepszy, jak cała reszta tego forum...

Adamm: "prawdziwy matematyk" = geometra

ElizaR: @aga: kiedyś byli .... ludzie z polotem i intuicją. Do dziś pamiętam genialne rozwiązania niektórych dawnych forumowiczów... @Adamm: Niekoniecznie. Ale w sposobie podejścia do problemów geometrycznych ujawnia się cała kultura matematyczna rozwiązującego jego doświadczenie, obycie z matematyką i talent. Oraz niezbędny w uprawianiu tej dyscypliny upór...

zxy: cóż.... nie zgodzę się z tą nierównością, albowiem dla trójkąta równobocznego o boku długości a mamy

	1		1		a√3		√3
r=		h=		•		=		a
	3		3		2		6

	2		2		a√3		2√3
R=		h=		•		=		a
	3		3		2		6

1		1		3
	p=		(a+a+a)=		a
2		2		2

wówczas

	√3		2√3		3√3		√3		3		1
r+R=		a+		a=		a=		a <		a=		p
	6		6		6		2		2		2

Blee:

	1		a+a+a
zxy		p =
	2		2*2

ElizaR: Mogę mieć przynajmniej taką satysfakcję, że ktoś czyta te posty... Ale to ogólnie jest rozczarowujące: marzyła mi się podniecająca dyskusja, a tymczasem − póki co − zgłosił się jedynie kontestator, w dodatku niemający racji... @zxy i innych: Nie wiedzieć czemu w polskiej matematyce szkolnej celebruje się ( wypisując explicite) miarę boku trójkąta równobocznego ( na przykład równą a) . Tymczasem, w wielu wypadkach dużo praktyczniej byłoby założyć, że ten bok ma długość 1. ( Podobnie niekiedy łatwiej jest prowadzić rachunki posługując się okręgiem czy sześcianem jednostkowym...). Przeskalowanie ( pomnożenie wszystkich parametrów przez dowolną stałą dodatnią ) zawsze generalizuje potem zagadnienie... O ile w zachodnich podręcznikach uczniowie są systematycznie przyzwyczajani do takiego podejścia, u nas króluje obyczaj iście przedpotopowy...

mat: ElizaR czy to LWG? Albo znacie sie?

mat:

	P
r=		, gdzie P−pole
	p

	a
R=		− twierdzenie sinusów
	2sinα

	1
P=		bcsinα
	2

zatem

	bcsinα		a
r+R=		+
	2p		2sinα

	r+R
nierownosc między średnimi:		≥√rR
	2

	bcsinα	a
czyli r+R≥2√
	2p	2sinα

	1		abc
r+R≥2*		√
	2		p

	abc
r+R≥√
	p

Jak sie gdzieś po drodze nie pomyliłem, to jest coś takiego, może coś pomoże

mat:

	√3		3
dla trojkąta rownobocznego wychodzi		a>√		a
	2		2

√3
	=0.8660254
2

	3
√		=0.8164966
	2

wiec nierownosc by byla całkiem przyzwoita

PW: Ja mam złośliwe pytanie do ElizyR. − Piszesz pracę licencjacką i szukasz pomocy na forum dla licealistów i gimnazjalistów? Jeżeli nie, to umieszczanie tu takiego problemu jest niepotrzebnym popisem (dowód Blundona, he he). Marzy ci się "podniecająca dyskusja"? To nie to forum.

Adamm: wystarczy wykazać że nie istnieje trójkąt dla którego p/2 = r+R

ElizaR: @mat: Bardzo Ci dziękuję za zainteresowanie. Dla trójkąta równobocznego jak i pitagorejskiego ( 3, 4, 5) Sprawdza się oszacowanie: r + R ≥ √^abc_p > ¹₂ p Należy więc przypuścić, że zadziała dla wszystkich trójkątów... Należy przeto udowodnić, że √^abc_p > ¹₂ p , czyli,że 32 abc > ( a + b + c )³ Szukamy dalej...

mat: dla wszystkich liczb dodatnich tak nie jest, np a=10, b=c=1 wtedy 32abc=320 (a+b+c)³=1728 więc istotnie trzeba będzie skorzystać z nierówności trójkąta (a+b>c, a+c>b, b+c>a)

ElizaR: @PW: Riposta : Nie piszę pracy naukowej. Bawię się matematyką. W trakcie urlopu. Są tacy jeszcze ludzie (np. ja), którzy potrafią się bawić czymś innym, niż smartfonem lub facebookiem... Nauczono mnie czytać. Także w językach obcych ( angielski, francuski, rosyjski, niemiecki...) .Umiem korzystać z internetu i stawiać SKUTECZNE pytania wyszukiwarce. w tym również w zakresie zagadnień matematycznych... Nierówność Blundona wyskoczyła w trakcie takich poszukiwań. To tyle. Chorobliwa podejrzliwość jest produktem chorej ( spaczonej ) wyobraźni. A tak na marginesie: zbieżność jednostajna ciągu funkcyjnego, czy wyznaczanie rzędu macierzy ( dla zbadania rozwiązalności układu równań liniowych), bądź wyznaczanie całek − a takie posty się tu pojawiają obok stricte gimnazjalno−licealnych pytań − nie wskazują, że to forum przeznaczone jest li−tylko do użytku typowo szkolnego...

Smietana: @ElizaR good for you

mat: myśle ze PW bardziej chodziło o to (z czym troche ciezko sie nie zgodzic), ze rzuciałaś jakis ,,problem" i potem: Gdzie się podziali prawdziwi matematycy na tym forum? Nie ma co atakowac forumowiczow, tym bardziej ze sama nie zaproponowalas nic procz postawienia problemu i jakiegos artykułu. Nie pisze tego złośliwie Czasem nawet ,,proste" problemy okazują sie trudniejsze niż sie wydaje: Jak hipoteza Goldbacha... Więc cierpliwości

ElizaR: @mat: jeśli chcesz tak naprawdę wiedzieć, to ta nierówność "wyskoczyła" jako produkt uboczny innego problemu, nad którym pracowałam, i bez wielkiego znaczenia dla logiki rozwiązania owegoż problemu ( bo prawa strona okazała się majorantą nierówności Blundona ), ale stanowi sama w sobie ciekawe zagadnienie, które postanowiłam zawiesić na tym forum...Zadanie oczywiście nie jest łatwe, ani oczywiste − w przeciwnym razie nie konferowałabym z Wami wszystkimi... Czekam cierpliwie i dziękuję raz jeszcze, «mat» za Twój trud!

ElizaR: Jeżeli zamienimy zmienne: a = x + z, b = x + y, c = y + z innymi słowy: x = ^a+b−c₂, y = ^b+c−a₂, z = ^a+c−b₂, to z nierówności trójkąta dla a, b, c mamy x, y, z − dodatnie, a nasza nierówność przyjmuje postać: 4( x + z )( x + y )( y + z ) > ( x + y + z )³

jc: Dla x=y=1/8, z=3/4 mamy L=4*(2/8)*(7/8)*(7/8)=(7/8)² < 1 P=1³=1, a więc trzeba szukać innej drogi...

ElizaR: tak zauważylam to już godzinę temu, niestety... Otrzymany wynik przez mat−a się nie interpoluje...

mat: wtedy

	7
a=
	8

	2
b=
	8

	7
c=
	8

nie jest spełniona nierownosc trojkąta: b>a+c

jc: Nie lubię takich zadań, ale poszukałem w malutkiej książce o trójkątach (60 stron 16x12 cm). Pod koniec znalzłem coś takiego: p² ≤ R² +4Re+3r²=4(R+r)²−(4Rr+3r²)<4(R+r)² Autorzy powołują się na nierówności z pierwszych stron książki.

jc: mat, z odcinków 7,7,2 bez kłopotu zbudujesz trójkąt.

mat: tak, głupote napisałem

ElizaR: @jc: nierówność p² ≤ R² +4Rr+3r² to dość znana u specjalistów nierówność GERRETSENA. W sposób natychmiastowy otrzymać z niej można zarówno naszą nierówność, ( co pokazałeś ), jak i nierówność Blundona.( wtedy jeszcze trzeba użyć nierówności Eulera).Sęk w tym, że nierówność Gerretsena wyprowadza się w dość skomplikowany sposób. ( por. np. https://math.stackexchange.com/questions/1843214/proving-gerretsens-inequality ) Mamy wynikania: Gerretsen → Blundon→nasza nieróność Gerretsen→ nasza nierówność Blundon (bezpośredni dowód, do którego podałam link w drugim poście) → nasza nierówność Ja szukam BEZPOŚREDNIEGO, prostego, dowodu naszej nierówności...Skoro bowiem można wyprowadzić bezpośrednio Blundona, to myślę, że można i też naszą nierówność... Niemniej dziękuję Ci , jc, za trud jaki sobie zadałeś. I... szukamy dalej!

ElizaR: Tak naprawdę dowód wystarczy przeprowadzić dla trójkąta rozwartokątnego; W przypadku trójkąta prostokątnego nierówność staje się trywialna jeśli wyrazimy wszystkie wielkości za pomocą przeciwprostokątnej i funkcji trygonometrycznych jednego z kątów ostrych; W przypadku trójkąta ostrokątnego korzystamy z równości: AH + BH + CH = 2(R + r) gdzie A, B, C − to wierzchołki trójkąta, a H jego ortocentrum ( dowód trygonometryczny). Następnie rozważamy nierówność trójkąta dla trójkątów AHB, BHC, CHA, i dodajemy je stronami... Pozostaje przypadek trójkąta rozwartokątnego.(Tu niestety AH + BH + CH ≠ 2(R + r)...) Będę niezmiernie wdzięczna za pomoc...

ElizaR: ?

ElizaR: ?

ElizaR: Czy ktoś jeszcze nad tym pracuje ?

zombi: Wrzuć na stacka może

jc: Rozumiem, że oczekujesz krótkiego bezpośredniego dowodu. Dowód we wspomnianej przeze mnie książce zajmuje pewnie 2 strony (ale małego formatu). Nie czytałem. Trochę myślałem, jakieś pomysły mam, ale przy obecnej temperaturze, nie jest łatwo.

ElizaR: @jc. Z czystej ciekawości: o jakiej książeczce mówisz? ( autor, tytuł...) sądząc po formacie to musi być jakaś rosyjska...Albo rumuńska...Z chęcią przeczytałabym. Podaj mi proszę namiary bibliograficzne. Spróbuję to sama znaleźć. Będę niezmiernie zobowiązana. Interesują mnie bowiem od zawsze w matematyce rozmaite strategie dowodzenia danego twierdzenia ...A jak na nierówność Gerretsena 2 strony to i tak krótko. Tyle,że trzeba zobaczyć, czy po drodze są jakieś lematy, dowodzone w innym miejscu publikacji... Dziękuję z góry! @zombi: myślałam o tym, jeszcze czekam...

jc: https://edu-lib.com/matematika-2/dlya-shkolnikov/v-p-soltan-s-i-meydman-tozhdestva-i-neravenstva-v-treugolnike

ElizaR: @jc : Bardzo Ci dziękuję!

ElizaR: I to zresztą jest ten fascynujący aspekt tej dyskusji: poznałam coś, czego nie znałam, cieszę się bardzo!

ElizaR: @jc. Nierówność Gerretsena w książce jest wyprowadzona standardowo...

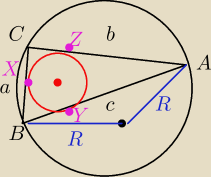
Milo: Na wstępie chciałbym bardzo bardzo przeprosić za rysunek, ale naprawdę nie umiem się tym sprawnie posługiwać Dla trójkąta rozwartokątnego: Chcemy pokazać, że r + R > 1/2p, czyli po prostu r + R > 1/4(a+b+c) czyli a + b + c < 4r + 4R Wprowadźmy jeszcze oznaczenia, których nie chciałem umieszczać na rysunku, by kompletnie go nie zepsuć: O − środek okręgu opisanego, S − środek okręgu wpisanego Dla pewności − X, Y, Z to punkty styczności okręgu wpisanego z bokami a c b odpowiednio, a kąt który powinien wyglądać jak rozwarty, to ten przy wierzchołku C c < 2R z prostej nierówności trójkąta (dla trójkąta ABO) BX = BY − jasne, chociażby z tw. Pitagorasa czy przystawania trójkątów Tak samo jasne, że AZ = AY Czyli BX + AZ = BY + AY = c < 2R Pozostaje pokazać, że XC + CZ < 4r Czyli, że XC < 2r Rozważmy trójkąt CXS i dla wygody niech x = XC Chcemy x < 2r. Kąt XCS jest połową kąta rozwartego, a kąt CSX − połową kąta ostrego. (bo miara kąta CSX to 180 stopni minus miara kąta XCS) Znanym faktem jest, że w trójkącie bok najdłuższy leży naprzeciw kąta o największej mierze, a najkrótszy − najmniejszej (chociażby z tw. sinusów, chociaż jestem pewien, że to znacznie prostszy fakt) Bez wątpienia zatem kąt XCS ma większą miarę niż CSX A zatem bok naprzeciw XCS (r) jest dłuższy, niż naprzeciw CSX (x) Czyli x < r < 2r Tyle wypociłem na tę chwilę. Jest późno, a ja z geometrii to raczej taka noga jestem, szczególnie po roku przerwy, więc mam przekonanie graniczące z pewnością, że jest tu gdzieś błąd. Wstawiam jednak w nadziei, że może jest on do znalezienia i wyeliminowania, lub że moje rozumowanie kogoś zainspiruje. A ponieważ − jako się rzekło − jest późno − dobranoc wszystkim

Milo: Już widzę głupotę − w moim wykonaniu czworokąt CXSZ ma sumę kątów wewnętrznych ponad 360 stopni. Czyli druga część rozumowania nie działa.

Milo: Nie, jednak post z 00:21 to głupota. Naprawdę idę spać, dobranoc i przepraszam za zamęt

ElizaR: @Milo: Dziękuję CI bardzo za włożony trud. NIestety Twoje rozumowanie nie daje ogólnej odpowiedzi na postawione zagadnienie... Chciałeś pokazać, że x = XC < 2r Ale ΔCXS jest prostokątny w X ( X jest punktem stycznośći; SX ⊥ BC ... ), i SX = r. Oznaczmy ∡ACB = γ, wtedy ∡ XCS = γ/2 i mamy: x = r ♦ ctg (γ/2) Aby było x = r ♦ ctg (γ/2) < 2r musiałoby być ctg (γ/2) < 2, co jest prawdą TYLKO dla kątów γ WIĘKSZYCH niż ok. 126^o30' Dla dużej części kątów rozwartych trójkąta nierówność udowodniłeś, ale co zrobisz z przedziałem ( 90^o; ca126^o30'] ?

ElizaR: Szukamy dalej...

ElizaR: Innymi słowy na polu bitwy pozostał przedział: ( π/2 ; arc ctg 2 ] .....

ElizaR: Błąd drukarski: ( π/2 ; 2 arc ctg 2 ] oczywiście...

ElizaR: Witam wszystkich... Najciemniej jest pod latarnią... Zwłaszcza jak człowiek jest ślepy! I tępy (mówię osobie, oczywiście...) MILO tak naprawdę udowodnił twierdzenie... (Sam zresztą o tym nie wiedząc). Pisząc komentarz do jego rozumowania pomyliłam się w rachunkach. Co zastopowało nas na całą dobę. Powróćmy przeto do tegoż komentarza z 21 sierpnia, z godziny 08:51... Rozwiązaniem nierówności ctg (γ/2) < 2 jest warunek γ/2 > arc ctg 2 ( bo funkcja ctg x jest malejąca na ( 0; π/2) ), Skąd γ > 2 arc ctg 2 ≈ 53^o I to jest bardzo dobra wiadomość. Rozumowanie Mila okazuje się prawdziwe NIE TYLKO dla trójkątów rozwartokątnych, ale też dla tych pozostałych, w których największy kąt przekracza 2 arc ctg 2 ≈ 53^o . A ponieważ udowodniliśmy uprzednio, że nierówność jest prawdziwa dla wszystkich kątów ostrych, suma mnogościowa rozpatrzonych przedziałów dowodzi prawdziwości nierówności dla wszystkich trójkątów. Że też nikt z forumowiczów nie zauważył mojego oczywistego błędu ! Podsumowując dyskusję: Dziękuję wszystkim tym, którzy wzięli w niej udział. Do zobaczenia w nowych postach! ADDENDUM: przekształcając nierówność wyjsciową do postaći R + r 1 + r/R −−−−−− > 1/2 ⇔ −−−−−−−−− > 1/2 r r/R Oraz uwzględniając fakt, iż 1 + r/R = cosA + cosB + cosC oraz r/R = sinA + sinB + sinC ( w każdym trójkącie ) udowodniliśmy nierówność "olimpijską" cosA + cosB + cosC −−−−−−−−−−−−−−−−−−− > 1/2 . sinA + sinB + sinC

ElizaR: Emenacja ( to ze zmęczenia; nie spałam dlugo dziś...) R + r 1 + r/R −−−−−−− > 1/2 ⇔ −−−−−−−−−− > 1/2 p p /R p /R = sinA + sinB + sinC

jc: Próbowałem wywnioskować coś z równości a+b+c = 2R(sin A + sin B + sin C) = 2r(ctg A/2 + ctg B/2 + ctg C/2)