równania i nierówności trygonometryczne karola: Rozwiąż równanie i nierówności: a) 1−tgx=cos2x,

	cos2x
b)		≤1 , x∊<0,2π>.
	cosx

Zupełnie nie wiem jak mam to rozpisać

Mila: 1)

	sinx		π
sin2x+cos2x−		=cos2x−sin2x i cosx≠0⇔x≠		+kπ, k∊C
	cosx		2

	sinx
⇔2sin2x−		=0
	cosx

2sin²x*cosx−sinx=0⇔ sinx*(2sinxcosx−1)=0⇔ sinx=0 lub sin2x=1 i x∊D Dokończ

karola:

	π		π
x=kπ v x=		+kπ i x≠		+kπ , k∊C
	4		2

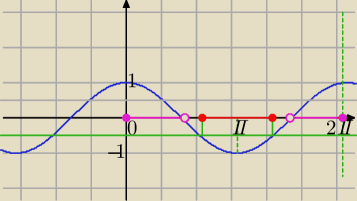Mila: 2)

cos(2x)		π
	≤1 i x∊<0,2π> i x≠		+kπ
cosx		2

2cos2x−1
	≤1
cosx

2cos2x−1
	−1≤0
cosx

2cos2x−1−cosx
	≤0
cosx

cosx=t i |t|≤1 i t≠0 (2t²−t−1)*t≤0 Δ=9

	1
t=−		lub t=1
	2

	1
t∊<−1,−		> lub t∊(0,1)
	2

	1		3π
cosx∊<−1,−		> lub cosx∊(0,1> i x≠U{π}2} i x≠		⇔
	2		2

	π		2π		4π		3π
x∊<0,		) ∪<		,		>∪(		,2π>
	2		3		3		2