Trygonometria , wykres , wartość bezwzględna , nie ogarniam kacpi666xd: Naszkicuj wykres funkcji f(x)=| tg(π/2−x) |−1 gdzie x€(−2π,−π)U(−π,0)U(0,π). Na podstawie wykresu wyznacz : a) miejsca zerowe funkcji f b) zbiór rozwiązań nierówności f(x+π/4)<0 . Proszę o wytłumaczenie bo naprawdę nie mogę ogarnąć jak to zrobić

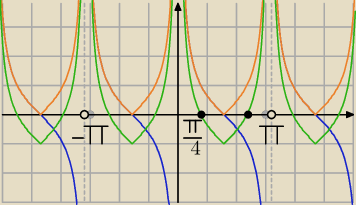
iteRacj@: 1/ naszkicuj wykres funkcji f(x)=|tg(π/2−x)|−1 gdzie x∊(−2π,−π)U(−π,0)U(0,π) mamy dwie możliwości: a/ zauważyć, że tg(π/2−x)=ctg(x) i narysować jako wyjściową funkcję g(x)=ctg(x)=tg(π/2−x), następnie wartość bezwzględną tej funkcji h(x)=|ctg(x)|=|tg(π/2−x)| i na koniec przesunąć wykres o wektor [0,−1], żeby otrzymać f(x)=|ctg(x)|−1=|tg(π/2−x)|−1

the foxi: Zauważ, że tg(π/2−x)=ctg(x). f(x)=ctg(x) f(x)=|ctg(x)| − to, co poniżej osi OX, odbij symetrycznie do góry f(x)=|ctg(x)|−1 − cały wykres obniż o 1 Kolejna kwestia − dziedzina x∊(−2π,−π)U(−π,0)U(0,π) to po prostu x∊(−2π;π)\{−π;0} I lecisz: a) miejsca zerowe, czyli rozwiąż f(x)=0 b) f(x+π/4)=|ctg(x+π/4)|−1 zatem rozwiąż nierówność |ctg(x+π/4)|−1<0 w razie pytań, pisz

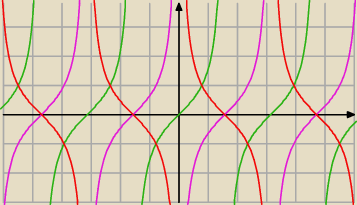
iteRacj@: b/ narysować jako wyjściową funkcję g(x)=tg(x),

	π
następnie przesunąć wykres o wektor [		,0] otrzymując h(x)=tg(x−π/2)
	2

i na koniec symetrycznie odbić wykres względem osi OX, żeby otrzymać k(x)=−tg(x−π/2)=tg(π/2−x)=ctg(x) i przejść do wykonania przekształceń z punktu a/

kacpi666xd: Dziękuję wam bardzo! Dwa dni się męczyłem z tym . Pozdrawiam serdecznie!

the foxi:

kacpi666xd: Czemu tg(π/2−x)=ctgx?

kacpi666xd: A , dobra . Ogarniam .