pole koła Marcin: Dany jest trójkąt o bokach długości 7,8,9 Oblicz pole koła które jest styczne do dwu krótszych boków i jego środek znajduje się na najdłuższym boku. Nic mi nie wychodzi pomoże ktoś?

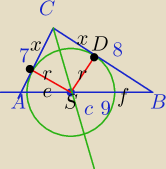Mila: |AS|=e, |BS|=f 1)

e		7
	=		z tw. o dwusiecznej kąta w trójkacie
f		8

7
	f+f=9
8

15
	f=9
8

	24		21
f=		, e=
	5		5

2) P_ΔABC:

	7+8+9
p=		=12
	2

P_ΔABC=√12*(12−7)*(12−8)*(12−9)=√12*5*4*3=12√5

	1
12√5=		*8*9*sinB
	2

	√5
sinB=
	3

3) W ΔSDB:

	r
sinB=
	f

r=f*sinB

	24		√5
r=		*
	5		3

	8√5
r=
	5

	64
Po=π*
	5

=========== Posprawdzaj rachunki.

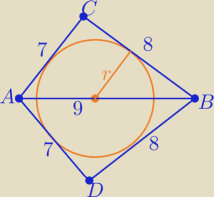Eta: 2 sposób Ze wzoru Herona : PΔABC = √12(12−7)(12−8)(12−9)= 12√5 ( jak u Mili P(deltoiduACBD)=2*P(ABC)= 24√5

	14+16		Pd		24√5		8√5
Pd=r*p , p=		=15 r=		=		=
	2		p		15		5

P_k=πr²

	64
Pk=		π [j2]
	5

============