Przykład - czy da się rozwiązać Przemek: Mam taki wielomian x⁷ − 2x³ − x >= 0 Jest on podany jako przykład wielomianu w necie i próbowałem go rozwiązać, ale nie daje rady. Zrobiłem tak: x(x⁶ − 2x² − 1) >= 0 Z tego nasze jedno miejsce zerowe jest w zerze. Próbowałem znaleźć drugie miejsce, ale nie niestety nie ma tego z twierdzenia z resztą że powinno to być 1 lub −1. Można to jeszcze zamienić na −x + x(x³+√2x)(x³−√2x) >= 0, ale też nic nie daje. Jak mam ustalić kolejne miejsce zerowe skoro f(1) = −2 i f(−1) =−2, a dla f(2) = 110, a f(−2) = −110 Może nie znam jakiegoś twierdzenia dopiero raczkuje w rozszerzeniu ^^

Saizou : Podstawmy za x²=t, mamy wówczas t³−2t−1=0 Łatwo zauważyć że − 1 jest rozwiązaniem tego rownania Myślę że dalej sam dasz radę PS. I nie z twierdzenia o reszcie, a z tw. O pierwiastkach wymiernych wielomianu

Przemek: Oke. Wyszło mi więc: x(x²+1)(t²−t−1) >= 0

	1+√5		1−√5
Więc x = 0 ; x2=/=−1 ; a z delty wychodzi t1 =		i t2 =		.
	2		2

	1+√5		1+√5		1−√5
Skoro x2 = t więc x1 = −		lub		,a x2 = −		lub
	2		2		2

	1−√5
	2

Wtedy trzeba rozpatrzyć przedziały dla 4 rozwiązań? Btw: Całkowicie zapomniałem że mogłem sobie t podstawić ^^

Przemek: Oczywiście te x1 i x2 jeszcze całe pod pierwiastkiem czyli:

	1+√5		1+√5
x1 = − √		lub √
	2		2

	1−√5		1−√5
x2 = −√		lub √
	2		2

Saizou : t2 odpada bo t>=0, wynika to z postawienia t=x² (kwadrat nie może być ujemny)

	1+√5
Więc zostaje x2=
	2

Przemek: No tak masz rację z tym. Przecież nie można wyciągnąć pierwiastka z minusa ^^. W takim razie

	1+√5
x1 = √
	2

	1+√5
x2 = −√
	2

Więc rozwiązanie to?:

	1+√5		1+√5
xE < −√		; 0 > i < √		; +nieskonczonosc )
	2		2

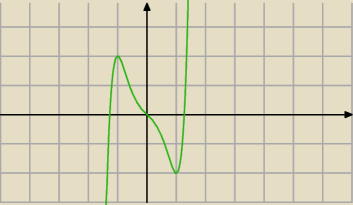
Saizou : W teorii i praktyce można wyciągnąć pierwiastek parzystego stopnia z liczby ujemnej, ale na razie nie zaprzątaj sobie tym głowy

PW: Przemku, nie pisz "rozwiązanie to

	1+√5		1+√5
<−√		, 0> i <1, √		,∞)",
	2		2

bo to ewidentny błąd logiczny − użycie spójnika "i" powoduje, że zbiór jest pusty.

Przemek: Saiozu az jestem ciekawy jak Moze dojde do tego bo jestem dopiero w polowie materialu rozszerzenia. PW Wiem wlasnie chcialem zmienic na lub ale nie mozna edytowac. Nie wiedzialem jak zrobic ten znaczek przypominajacy u wiec dalem po prostu i xd

Saizou : Przemek nad okienkiem wpisywania masz różne symbole, jeśli klikniesz wybrany, to się wstawi do tekstu. Jeśli brakuje Ci jakiegoś "znaczka" kliknij w inne, tam jest ich więcej Jeśli chcesz rysować, kliknij rysuję